
【题目】如图,在平行四边形ABCD中,点O是对角线AC上一点,连接BO、DO,△COD、△AOD、△AOB、△BOC的面积分别是S1、S2、S3、S4.下列关于S1、S2、S3、S4的等量关系式中错误的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
如图,分别过B、D作BF⊥AC于F,DE⊥AC于E,根据平行四边形的性质可得CD//AB,可得∠DCA=∠BAC,CD=AB,利用AAS可证明△CDE≌△ABF,可得DE=BF,根据等底等高的三角形面积相等即可得出S1=S4,S2=S3,进而对各选项逐一判断即可得答案.
如图,分别过B、D作BF⊥AC于F,DE⊥AC于E,
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∴∠DCE=∠BAF,
在△CDE和△ABF中,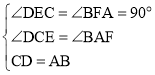 ,
,
∴DE=BF,
∴![]() OA·DE=
OA·DE=![]() OA·BF,
OA·BF,![]() OC·DE=
OC·DE=![]() OC·BF,即S1=S4,S2=S3,
OC·BF,即S1=S4,S2=S3,
∴S1+S3=S2+S4,![]() ,
,![]() ,故A、B、C选项正确,
,故A、B、C选项正确,
只有OA=2OC时,S2=2S1,故D选项错误,
故选:D.


科目:初中数学 来源: 题型:
【题目】 如图,Rt△ABC中,∠C = 90°,把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,点E在AB上.
(1)若∠BDA = 70°,求∠BAC的度数.
(2)若BC = 8,AC = 6,求△ABD中AD边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图

(1)分别写出下列各点的坐标:A′______;B′______;C′______
(2)若点P(m,n)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为______.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在方格中,位置如图,A点的坐标为(﹣3,1).

(1)写出B、C两点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1;
(3)在x轴上存在点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)平移后的三个顶点坐标分别为:.A1( ),B1( ),C1( ).
(2)在上图中画出平移后三角形A1B1C1;
(3)画出△AOA1并求出△AOA1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
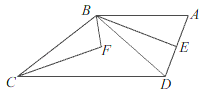
A. 115° B. 110° C. 105° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点M是BE的中点,连接CM、DM.

(1)当点D在AB上,点E在AC上时(如图一),求证:DM=CM,DM⊥CM;
(2)当点D在CA延长线上时(如图二)(1)中结论仍然成立,请补全图形(不用证明);
(3)当ED∥AB时(如图三),上述结论仍然成立,请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)CD与EF平行吗?并说明理由;
(2)若∠A=72°,求∠FEC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com