Question

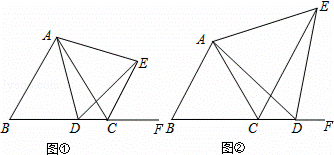
已知等边△ABC，点D是直线BC上一点，以AD为边在AD的右侧作等边△ADE，连结CE．

（1）如图①，若点D在线段BC上，求证：CE+CD=AB；

（2）如图②，若点D在BC延长线上，线段CD，CE和AB有怎样的数量关系？证明你的结论．

Answer 1

证明：（1）如图①，∵△ADE与△ABC都是等边三角形，

∴AC=AB，AE=AD，∠DAE=∠BAC=60°．

∴∠DAE﹣∠CAD=∠BAC﹣∠CAD．

即∠CAE=∠BAD．

在△CAE和△BAD中，

，

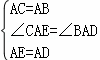∴△CAE≌△BAD（SAS）．

∴EC=DB（全等三角形的对应边相等）；

∴CE+CD=DB+CD=BC=AB，

即CE+CD=AB；

（2）CE﹣CD=AB；

理由如下：如图②，∵△ADE与△ABC都是等边三角形，

∴AC=AB，AE=AD，∠DAE=∠BAC=60°．

∴∠DAE+∠CAD=∠BAC+∠CAD．

即∠CAE=∠BAD．

在△CAE和△BAD中，

，

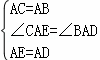∴△CAE≌△BAD（SAS）．

∴EC=DB（全等三角形的对应边相等）；

∴CE﹣AB=DB﹣BC=CD，即CE﹣CD=AB．