
����Ŀ���ۺ���̽������ͼ����֪������y����x2��bx��c��һֱ���ཻ��A(��1��0)��C (2��3)���㣬��y�ύ�ڵ�N���䶥��ΪD ��
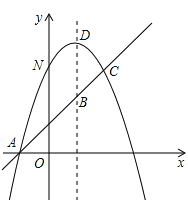
��1��ȷ��������ֱ��AC�ĺ�����ϵʽ��
��2����M��ֱ��x =3�ϣ���ʹ MN��MD ��ֵ��Сʱ��M�����ꣻ
��3���������ߵĶԳ�����ֱ��AC �ཻ�ڵ�B��E Ϊֱ��AC �ϵ�����һ�㣬����E ��EF��BD ���������ڵ�F����B��D��E��F Ϊ������ı����ܷ�Ϊƽ���ı��Σ����ܣ����E �����ꣻ�����ܣ���˵�����ɡ�
���𰸡���1��y=-x2+2x+3��ֱ��ACΪy=x+1����2��M��3��![]() ������3��E��0��1����
������3��E��0��1����![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��������
�����������1������A��C��������������߽���ʽ�ɵó�b��c��ֵ���̶��ó������߽���ʽ�����ô���ϵ���������AC�ĺ�������ʽ��
��2��������Գ������·����֪ʶ���ҵ�N�����ֱ��x=3�ĶԳƵ�N��������N'D��N'D��ֱ��x=3�Ľ��㼴�ǵ�M��λ�ã��̶����m��ֵ��
��3�������E�����꣬��������ۣ�������E���߶�AC��ʱ����F�ڵ�E�Ϸ���������E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·�������ƽ���ı��ε����ʱ�ʾ��F�����꣬����F��������������߽���ʽ�ɵó�x��ֵ���̶������E�����꣮
�����������1����������y=-x2+bx+c����A��-1��0����C��2��3�����ɵã�
![]() ����ã�
����ã�![]() ��
��
��������Ϊy=-x2+2x+3��
��ֱ��AC����ʽΪy=kx+n������A��-1��0����C��2��3������ã�
![]() ����ã�
����ã�![]() ��
��
��ֱ��ACΪy=x+1��
��2����N�����ֱ��x=3�ĶԳƵ�N������N����6��3�����ɣ�1����D��1��4����
�����ֱ��DN���ĺ�����ϵʽΪy=-![]() x+
x+![]() ��
��
��M��3��m����ֱ��DN����ʱ��MN+MD��ֵ��С��
��m=-![]() ��3+
��3+![]() =
=![]() ��
��
��M��3��![]() ��
��
��3���ɣ�1������2����D��1��4����B��1��2��
��E��ֱ��AC�ϣ���E��x��x+1����
������E���߶�AC��ʱ����F�ڵ�E�Ϸ�����F��x��x+3����
��F���������ϣ�
��x+3=-x2+2x+3
��ã�x=0��x=1����ȥ����
���E����������0��1����
������E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·�����F��x��x-1����
����F���������ϣ�
��x-1=-x2+2x+3��
���x=![]() ��x=
��x=![]() ��
��
����E����������![]() ��
��![]() ����
����![]() ��
��![]() ��
��
���Ͽɵ����������ĵ�EΪE��0��1����![]() ��
��![]() ����
����![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���P�ڱ�CD�ϣ�����C��D���غϣ�����A��AP�Ĵ�����CB���ӳ����ཻ�ڵ�Q������PQ��MΪPQ�е㣮

��1����֤����ADP�ס�ABQ��
��2����AD=10��AB=20����P�ڱ�CD���˶�����DP=x��BM2=y����y��x�ĺ�����ϵʽ�������߶�BM����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ����������ֽ�糵��������
�Ķ�������ֽ�糵�����������̣�����������⣺������ֽ�糵��������������أ���ͼ1�����ȣ��ü�һ��߳�Ϊ12cm��������ֽ�ţ��������泯�£�ʹ����ij��ӣ��������Խ��ߣ�������Խ��߶��ۣ����ҵ��Խ��ߵĽ���O���ð�������������ǣ��ڱ�����O���ֳɵ������߶��Ͽ�������O�����ȷֵ㴦�ֱ�����ǣ���ͼ2��Ȼ���������ε�ÿ���ǿ�ʼ�ӶԽ����������ǺŴ�ͣ�£���������8�����۵��Ľǣ��������ڵ��ĸ��ǣ�������ָ�����м��һ�ǣ��������ģ�������˿���Ӱ����̶���һ��ľ���Ͼ��������ˡ�

����һ��
��1����ͼ2 �������������ڶԽ��������ñ�ǵ�ʾ��ͼ�������������ÿ���Ǵ��ضԽ������ij��ȣ�
��2�������ǵ�E��������ABCD�Ķ���B�ľ��롣
�������
�������ཻ��O��![]() �����������Ϊ���ཻ��O��
�����������Ϊ���ཻ��O��![]() ������������������ڵ��ĸ����۵���ѹƽ��ʹ�ǵĶ����뽻��O �غϣ������������䡣
������������������ڵ��ĸ����۵���ѹƽ��ʹ�ǵĶ����뽻��O �غϣ������������䡣
��1������ͼ3�У���������ֽ�糵����ʾ��ͼ���������������ص�����ͼ����Ӱ��
��2�������1���в����������������ֽ�糵��ʾ��ͼ���ص����ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ʽ2a2��3a��1��ֵ����6����ô����ʽ6a2��9a��5��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2����2��3����3���ĸ����У���С�����ǣ�������
A. 2 B. ��2 C. 3 D. ��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����: ![]() ,
,![]() ��
�� ![]() ����
����
��2��̽��(1)��ʽ�ӵĹ��ɣ���д����![]() ����ʽ����˵����
����ʽ����˵����![]() ����ʽ����:
����ʽ����:
��3������: ![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com