
【题目】综合与实践:“四扇纸风车”的制作
阅读“四扇纸风车”的制作过程,解决下列问题:“四扇纸风车”是如何制作的呢?如图1,首先,裁剪一块边长为12cm的正方形纸张;将花纹面朝下,使用你的尺子,画两条对角线(或沿其对角线对折);找到对角线的交点O,用按钉按下做个标记;在被交点O所分成的四条线段上靠近交点O的三等分点处分别做标记;如图2,然后由正方形的每个角开始延对角线剪开,到记号处停下;这样就有8个可折叠的角,将不相邻的四个角(不相邻指两角中间隔一角)折向中心;再用铁丝或钉子把它固定在一根木棍上就制作好了。

任务一:
(1)如图2 是制作过程中在对角线上做好标记的示意图,请求出正方形每个角处沿对角线剪开的长度;
(2)求出标记点E到正方形ABCD的顶点B的距离。
任务二:
若将“距交点O的![]() 处做标记”改为“距交点O的
处做标记”改为“距交点O的![]() 处做标记”并将不相邻的四个角折叠、压平,使角的顶点与交点O 重合,其余条件不变。
处做标记”并将不相邻的四个角折叠、压平,使角的顶点与交点O 重合,其余条件不变。
(1)请在图3中,把“四扇纸风车”的示意图补充完整,并将重叠部分图上阴影;
(2)求出(1)中补充完整后的“四扇纸风车”示意图中重叠部分的面积。
【答案】任务一:(1)![]() cm;(2)
cm;(2)![]() cm;任务二:(1)补图见解析;(2)
cm;任务二:(1)补图见解析;(2)![]()
【解析】
试题分析:任务一:(1)解直角三角形即可求解;(2)运用勾股定理求解即可;任务二:(1)补图即可;(2)由题意可知:重叠部分三角形是等腰直角三角形,且四个三角形的面积相等。求出一个,即可求出全面积.
试题解析:任务一:
(1)∵四边形ABCD是正方形,
∴![]()
在![]() 中,
中,![]() ∴
∴![]()
∴![]()
∴正方形每个角处沿对角线剪开的长度为![]() cm
cm
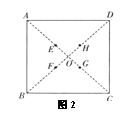
(2)连接BE,
∵四边形ABCD是正方形,![]()
∴![]()
∴![]()
∴标记点E到正方形ABCD的顶点B的距离为![]() cm。
cm。
任务二:
(1)如图所示:
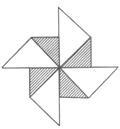
(2)由题意可知:重叠部分三角形是等腰直角三角形,且四个三角形的面积相等。
其中一块重叠部分的面积为:![]()
∴“四扇纸风车”示意图中重叠部分的面积为:![]()


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】综合与探究:如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C (2,3)两点,与y轴交于点N,其顶点为D 。
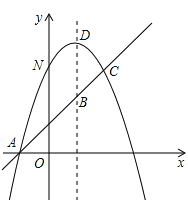
(1)确定抛物线及直线AC的函数关系式;
(2)点M在直线x =3上,求使 MN+MD 的值最小时的M点坐标;
(3)若抛物线的对称轴与直线AC 相交于点B,E 为直线AC 上的任意一点,过点E 作EF∥BD 交抛物线于点F,以B、D、E、F 为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
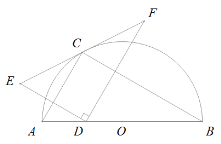
【题目】 如图点![]() 在以
在以![]() 为直径的半圆的圆周上,若
为直径的半圆的圆周上,若![]()
![]() 为边
为边![]() 上一动点,点
上一动点,点![]() 和
和![]() 关于
关于![]() 对称 ,当
对称 ,当![]() 与
与![]() 重合时,
重合时,![]() 为
为![]() 的延长线上满足
的延长线上满足![]() 的点,当
的点,当![]() 与
与![]() 不重合时,
不重合时,![]() 为
为![]() 的延长线与过
的延长线与过![]() 且垂直于
且垂直于![]() 的直线的交点,
的直线的交点,
(1)当![]() 与
与![]() 不重合时,
不重合时,![]() 的结论是否成立?试证明你的判断.
的结论是否成立?试证明你的判断.
(2)设![]() 求
求![]() 关于
关于![]() 的函数及其定义域;
的函数及其定义域;
(3)如存在![]() 或
或![]() 恰好落在弧
恰好落在弧![]() 或弧
或弧![]() 上时,求出此时
上时,求出此时![]() 的值;如不存在,则请说明理由.
的值;如不存在,则请说明理由.
(4)请直接写出当![]() 从
从![]() 运动到
运动到![]() 时,线段
时,线段![]() 扫过的面积.
扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com