
【题目】如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.

(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
【答案】(1)证明见解析;(2)y=![]() x2-20x+125(0<x<20).
x2-20x+125(0<x<20).![]() .
.
【解析】
试题分析:(1)由对应两角相等,证明两个三角形相似;
(2)如解答图所示,过点M作MN⊥QC于点N,由此构造直角三角形BMN,利用勾股定理求出y与x的函数关系式,这是一个二次函数,求出其最小值;
试题解析:(1)∵∠QAP=∠BAD=90°,
∴∠QAB=∠PAD,
又∵∠ABQ=∠ADP=90°,
∴△ADP∽△ABQ.
(2)∵△ADP∽△ABQ,
∴![]() ,即
,即![]() ,解得QB=2x.
,解得QB=2x.
∵DP=x,CD=AB=20,
∴PC=CD-DP=20-x.
如图所示,过点M作MN⊥QC于点N,
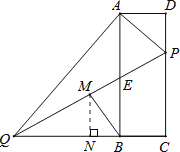
∵MN⊥QC,CD⊥QC,点M为PQ中点,
∴点N为QC中点,MN为中位线,
∴MN=![]() PC=
PC=![]() (20-x)=10-
(20-x)=10-![]() x,
x,
BN=![]() QC-BC=
QC-BC=![]() (BC+QB)-BC=
(BC+QB)-BC=![]() (10+2x)-10=x-5.
(10+2x)-10=x-5.
在Rt△BMN中,由勾股定理得:BM2=MN2+BN2=(10-![]() x)2+(x-5)2=
x)2+(x-5)2=![]() x2-20x+125,
x2-20x+125,
∴y=![]() x2-20x+125(0<x<20).
x2-20x+125(0<x<20).
∵y=![]() x2-20x+125=
x2-20x+125=![]() (x-8)2+45,
(x-8)2+45,
∴当x=8即DP=8时,y取得最小值为45,BM的最小值为![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。
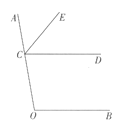
(1)依题意补全图形;
(2)若∠COB+∠OCD=180°,求证:∠ACE=∠COF。
请将下面的证明过程补充完整。
证明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE=______________,∠COF=![]() ∠COB。
∠COB。
(理由: _____________________________________)
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠____________。
(理由: ___________________________________)
∴∠ACE=∠COF。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店经销一种品牌服装,平均每天可销售20件,每件赢利44元,经市场预测发现:在每件降价不超过10元的情况下,若每件降价1元,则每天可多销售5件,若该专卖店要使该品牌服装每天的赢利为1600元,则每件应降价_________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C (2,3)两点,与y轴交于点N,其顶点为D 。
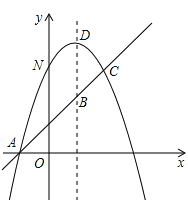
(1)确定抛物线及直线AC的函数关系式;
(2)点M在直线x =3上,求使 MN+MD 的值最小时的M点坐标;
(3)若抛物线的对称轴与直线AC 相交于点B,E 为直线AC 上的任意一点,过点E 作EF∥BD 交抛物线于点F,以B、D、E、F 为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com