练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某市推出电脑上网包月制，每月收取费用y（元）与上网时间x（小时）的函数关系如图所示，其中BA是线段，且BA∥x轴，AC是射线．

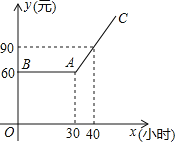
    （1）若小李11月份上网20小时，他应付多少元的上网费用？

    （2）当x≥30，求y与x之间的函数关系式；

    （3）若小李12月份上网费用为135元，则他在该月份的上网时间是多少？

    【答案】（1）60元；（2）y＝3x﹣30；（3）55个小时.

    【解析】

    （1）根据图像可知：每月上网30小时以内收费60元；超过30小时按超出时间多少收费；（2）20<60，故付费60元；（3）求y=135时，x的值即可.

    解：（1）根据题意，从图象上看，30小时以内的上网费用都是60元；

    （2）当x≥30时，设函数关系式为y＝kx+b，

    则，解得，

    故函数关系式为y＝3x﹣30；

    （3）由135＝3x﹣30解得x＝55，

    故12月份上网55个小时．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】周末，小明从家步行去书店看书.出发小时后距家1.8千米时，爸爸驾车从家沿相同路线追赶小明，在地追上小明后，二人驾车继续前行到达书店.小明在书店看书，爸爸去单位地办事.如图是小明与爸爸两人之间距离（千米）与小明出发的时间（小时）之间的函数图象，（小明步行速度与爸爸驾车速度始终保持不变，彼此交流时间忽略不计），请根据图象回答下列问题：

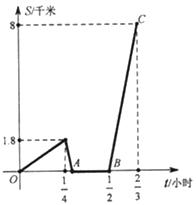
    （1）小明步行速度是_____千米/小时，爸爸驾车速度是______千米/小时：

    （2）图中点的坐标是______：

    （3）求书店与家的路程；

    （4）求爸爸出发多长时间，两人相距3千米.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点O为直线AB上一点，过O点作射线OC，使∠AOC：∠BOC＝1：2，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

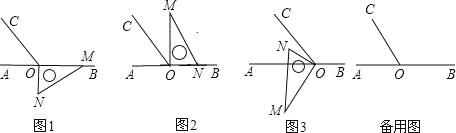
    （1）将图1中的三角板绕点O按逆时针方向旋转至图2的位置，使得ON落在射线OB上，此时三角板旋转的角度为　 　度；

    （2）继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置，使得ON在∠AOC的内部．试探究∠AOM与∠NOC之间满足什么等量关系，并说明理由；

    （3）在上述直角三角板从图1逆时针旋转到图3的位置的过程中，若三角板绕点O按15°每秒的速度旋转，当直角三角板的直角边ON所在直线恰好平分∠AOC时，求此时三角板绕点O的运动时间t的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知线段AB、a、b．

    （1）请用尺规按下列要求作图：（不要求写作法，但要保留作图痕迹）

    ①延长线段AB到C，使BC＝a；

    ②反向延长线段AB到D，使AD＝b．

    （2）在（1）的条件下，如果AB＝8cm，a＝6m，b＝10cm，且点E为CD的中点，求线段AE的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】新定义：若∠α的度数是∠β的度数的n倍，则∠α叫做∠β的n倍角．

    （1）若∠M＝10°21′，请直接写出∠M的3倍角的度数；

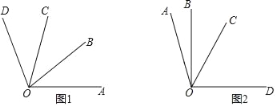
    （2）如图1，若∠AOB＝∠BOC＝∠COD，请直接写出图中∠AOB的所有2倍角；

    （3）如图2，若∠AOC是∠AOB的3倍角，∠COD是∠AOB的4倍角，且∠BOD＝90°，求∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点D是线段AB上的任意一点（不与点A和B重合），C是线段AD的中点，AB=4cm.

    （1）若D是线段AB的中点，求线段CD的长度.

    （2）在图中作线段DB的中点E，当点D在线段AB上从左向右移动时，试探究线段CE长度的变化情况.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

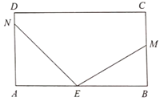
    【题目】如图，长方形纸片ABCD，点E在边AB上，M、N分别在射线BC和射线AD上，连接EM，EN，将三角形MBE沿EM折叠（把物体的一部分翻转和另一部分贴拢），点B落在点B’处；将三角形NAE沿EN折叠，点A落在点A’处.

    （1）若，，用直尺、量角器画出射线EB’与EA’；

    （2）若，，求的度数；

    （3）若，，用含的代数式表示的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

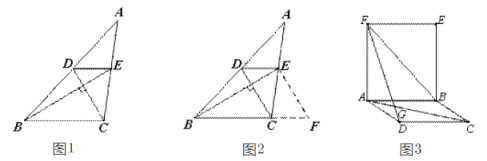
    【题目】阅读下面的材料：小锤遇到一个问题：如图①，在△ABC中，DE//BC分别交AB于点D，交AC于点E，已知CDBE，CD=2，BE=3，求BC+DE的值.

    小锤发现，过点E作EFDC，交BC的延长线于点F，构造△BEF，经过推理和计算能够使问题得到解决.

    （1）请按照上述思路完成小锤遇到的问题；

    （2）参考小锤思考问题的方法，解决下面的问题：如图②，四边形ABCD是平行四边形，四边形ABEF是矩形，AC与DF交于点G，AC=BF=DF，求∠DGC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在□ABCD中，E为BC的中点，过点E作EF⊥AB于点F，延长DC，交FE的延长线于点G，连结DF，已知∠FDG=45°

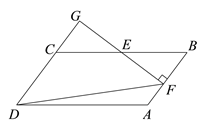
    （1）求证：GD=GF.

    （2）已知BC=10， .求 CD的长.

    查看答案和解析>>

    同步练习册答案