
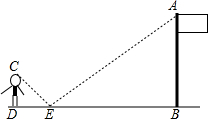
 如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.
如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度. 分析 根据反射定律可以推出∠CED=∠AEB,所以可得△BAE∽△DCE,再根据相似三角形的性质解答.
解答 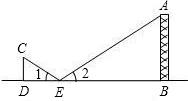 解:结合光的反射原理得:∠CED=∠AEB.
解:结合光的反射原理得:∠CED=∠AEB.
在Rt△CED和Rt△AEB中,
∵∠CDE=∠ABE=90°,∠CED=∠AEB,
∴Rt△CED∽Rt△AEB,
∴$\frac{DC}{AB}=\frac{DE}{EA}$,
即$\frac{1.65}{AB}$=$\frac{2}{12.8}$,
解得AB=10.56(m).
答:旗杆AB的高度是10.56m.
点评 本题考查相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.


科目:初中数学 来源: 题型:填空题
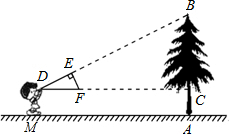 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度DM=150cm,CD=800cm,则树高AB=550cm.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度DM=150cm,CD=800cm,则树高AB=550cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
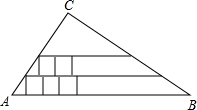 如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放22个.
如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放22个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com