
【题目】如图1是一款优雅且稳定的抛物线型落地灯,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,点最高点C距灯柱的水平距离为1.6米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为__米.

【答案】2.88.
【解析】
根据题意可以把AB所在的直线当作y轴,AE所在的直线当作x轴建立直角坐标系,由防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,最高点C距灯柱的水平距离为1.6米,可以知道抛物线的顶点坐标C(1.6,2.5),直接设出顶点式y=a(x1.6)2+2.5,然后用待定系数法将(0,1.5)代入解析式解得a值,再将D点到地面的高当作纵坐标代入解析式即可求出AE的长,将不符合实际的取值舍去即可.
根据题意可以把AB所在的直线当作y轴,AE所在的直线当作x轴建立直角坐标系,
∴设y=a(x﹣1.6)2+2.5,
∴把x=0,y=1.5代入上式得,1.5=a(0﹣1.6)2+2.5,
解得:a=﹣![]() ,
,
∴y=﹣![]() (x﹣1.6)2+2.5,
(x﹣1.6)2+2.5,
又∵DE的高为1.86米,
∴当y=1.86时,则﹣![]() (x﹣1.6)2+2.5=1.86,
(x﹣1.6)2+2.5=1.86,
解得,x=2.88或x=0.32(舍去),
故答案为:2.88.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个足球垂直地面向上踢,![]() (秒)后该足球的高度
(秒)后该足球的高度![]() (米)适用公式
(米)适用公式![]() .
.
(1)经多少秒时足球的高度为20米?
(2)小明同学说:“足球高度不可能达到21米!”你认为他说得对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂设计了一款成本为20元∕件的公益用品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)认真分析上表中的数据,用你所学过的函数知识确定一个满足这些数据的y与x的函数关系,并求出函数关系式.
(2)设该厂试销该公益品每天获得的利润为w元,当销售单价x定为多少时,w有最大值?最大利润是多少?
(3)当地民政部门规定,若该厂销售此公益品单价不低于成本价且不超过46元/件时,该厂每销售一件此公益品,国家就补贴该厂a元利润(a>4)。设日销售利润为m元,公司通过销售记录发现,m始终随销售单价x的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过点B(1,﹣3),对称轴是直线x=2,且抛物线与x轴的正半轴交于点A.
(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x的取值范图;
(2)在第二象限内的抛物线上有一点P,当PA⊥BA时,求△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-![]() .
.
(1)将y=-![]() +x+
+x+![]() 用配方法化为y=a(x-h)2+k的形式;
用配方法化为y=a(x-h)2+k的形式;
(2)求该函数图象与两坐标轴交点的坐标;
(3)画出该函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
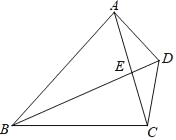
【题目】已知:如图,四边形ABCD的对角线AC和BD相交于点E,AD=DC,DC2=DEDB,求证:
(1)△BCE∽△ADE;
(2)ABBC=BDBE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com