
【题目】某厂设计了一款成本为20元∕件的公益用品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)认真分析上表中的数据,用你所学过的函数知识确定一个满足这些数据的y与x的函数关系,并求出函数关系式.
(2)设该厂试销该公益品每天获得的利润为w元,当销售单价x定为多少时,w有最大值?最大利润是多少?
(3)当地民政部门规定,若该厂销售此公益品单价不低于成本价且不超过46元/件时,该厂每销售一件此公益品,国家就补贴该厂a元利润(a>4)。设日销售利润为m元,公司通过销售记录发现,m始终随销售单价x的增大而增大,求a的取值范围.
【答案】(1)y=-10x+800 (2)50元/件;9000元 (3)60≥a≥8
【解析】
(1)直接运用待定系数法根据统计表的数据就可以求出y与x之间的函数关系式;
(2)设工艺厂试销该公益用品每天获得的利润是W元,先表示出每件的利润为(x-20),再根据总利润=单价利润×销售总量建立等式即可得出结论;
(3)设总利润为m元,根据条件可以得出每件工艺用品的利润为(x-20+a)元,再根据总利润=销售总价-成本总价建立函数关系式即可.
解:(1)设y与x之间的函数关系式为y=kx+b,根据统计表得![]() ,
,
解得:![]() ,故函数关系式是y=-10x+800;
,故函数关系式是y=-10x+800;
(2)设工艺厂试销该公益用品每天获得的利润是W元,依题意得
W=(x-20)(-10x+800)=-10x2+1000x-16000=-10(x-50)2+9000
则当x=50时,W有最大值9000.
故当销售单价定为50元∕件时,工艺厂试销该公益用品每天获得的利润最大,最大利润是9000元.
(3)设日销售利润为m元,则每件工艺用品的利润为(x-20+a)元,由题意,得
![]()
![]()
![]()
∵![]() ,
,
∴抛物线的开口向下,在对称轴的左侧m随x的增大而增大,
∴![]() 时,m有最大值,
时,m有最大值,
∵日销售利润m随销售单价x的增大而增大,且![]() ,
,
∴![]() ,解得
,解得![]() ,
,
又∵a>4
∴![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过50元,则至少需要用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.
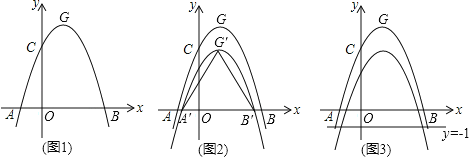
(1)求出抛物线C1的解析式,并写出点G的坐标;
(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
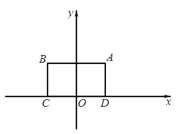
【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(![]() ,
,![]() ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.
(1)当⊙P的半径为4时,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
②如果点P在直线![]() 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
(2)已知点P在![]() 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
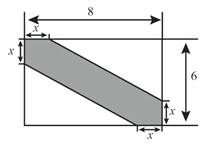
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一款优雅且稳定的抛物线型落地灯,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,点最高点C距灯柱的水平距离为1.6米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为__米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.

(1)求抛物线的解析式及A点坐标.
(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.
(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′、B′D
①当点B′落坐标轴上时,求点D的坐标.
②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月饼是久负盛名的中国传统糕点之一,宋代大诗人苏东坡有诗句“小饼如嚼月,中有酥和饴”赞美月饼.为满足市场需求,某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不低于45元且不超过58元,根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量![]() (盒)与每盒售价
(盒)与每盒售价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com