
【题目】将两块直角三角形纸板如图①摆放,![]() ,现将
,现将![]() 绕
绕![]() 点逆时针转动;
点逆时针转动;
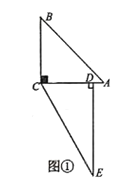
![]() 当转动至图②位置时,若
当转动至图②位置时,若![]() ,且
,且![]() 平分
平分![]() 平分
平分![]() ,则
,则![]() _;
_;
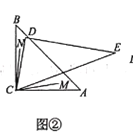
![]() 当转动至图③位置时,
当转动至图③位置时,![]() 平分
平分![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
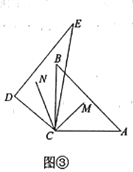
![]() 当转动至图④位置时,
当转动至图④位置时,![]() 平分
平分![]() 平分
平分![]() ,请直接写出
,请直接写出![]() 的度数.
的度数.
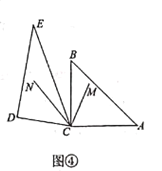
【答案】(1)75°;②75°;75°
【解析】
(1)先求出∠BCD,再根据角平分线的性质求出∠ACM和∠BCN,根据∠MCN=∠ACB-∠ACM-∠BCN计算即可得出答案;
(2)先根据角平分线的性质得出∠ACM=![]() ∠ACE,∠BCN=
∠ACE,∠BCN=![]() ∠BCD,再根据
∠BCD,再根据
![]() 代入求解即可得出答案;
代入求解即可得出答案;
(3)步骤同(2)一样.
解:(1)根据题意可得∠BCD=∠ACB-∠DCE-∠ACE=10°
又CM平分∠ACE,CN平分∠BCD
∴∠ACM=![]() ∠ACE=10°,∠BCN=
∠ACE=10°,∠BCN=![]() ∠BCD=5°
∠BCD=5°
∴∠MCN=∠ACB-∠ACM-∠BCN=75°
(2)∵CM平分∠ACE,CN平分∠BCD
∴∠ACM=![]() ∠ACE,∠BCN=
∠ACE,∠BCN=![]() ∠BCD
∠BCD
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)∵CM平分∠ACE,CN平分∠BCD
∴∠ACM=![]() ∠ACE,∠BCN=
∠ACE,∠BCN=![]() ∠BCD
∠BCD
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
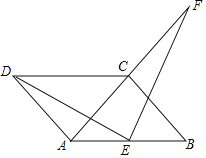
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
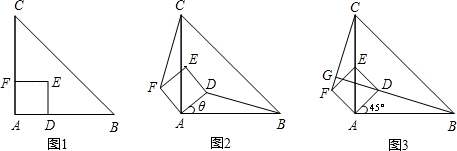
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF;
②当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )
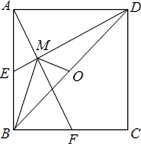
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
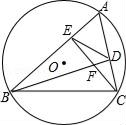
【题目】如图,⊙O的半径为2,弦BC=2![]() ,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:
,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:
①∠A始终为60°;
②当∠ABC=45°时,AE=EF;
③当△ABC为锐角三角形时,ED=![]() ;
;
④线段ED的垂直平分线必平分弦BC.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
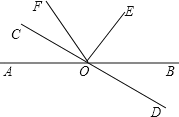
【题目】如图,直线![]() 、
、![]() 相交于
相交于![]() ,∠EOC=90°,
,∠EOC=90°,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求
,求![]() 的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
解:∵![]()
![]() ( )
( )
∴![]()
![]()
∵![]() 是
是![]() 的角平分线
的角平分线
∴![]()
![]() ( )
( )
∴![]()
![]()
∵![]()
![]()
![]() ( )
( )
∴![]()
![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型商场销售一种茶具和茶碗,茶具每套定价2000元,茶碗每只定价200元,“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案,方案一:买一套茶具送一只茶碗;方案二,茶具和茶碗按定价的九五折付款,现在某客户要到商场购买茶具30套,茶碗![]() 只(
只(![]() ).
).
(1)若客户按方案一,需要付款 元;若客户按方案二,需要付款 元.(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,试通过计算说明此时哪种购买方案比较合适?
,试通过计算说明此时哪种购买方案比较合适?
(3)当![]() ,能否找到一种更为省钱的方案,如果能是写出你的方案,并计算出此方案应付钱数;如果不能说明理由.
,能否找到一种更为省钱的方案,如果能是写出你的方案,并计算出此方案应付钱数;如果不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com