【题目】如图，四边形ABCD是一个正方形.

⑴请你在平面内找到一个点O，并连接OA、OB、OC、OD使得到△OAB、△BOC、△COD、△OAD都是等腰三角形.

⑵这样的点，你能找到多少个？

⑶试写出你找到的等腰三角形的顶角的度数.

参考答案：

【答案】(1)见解析；（2）9；（3）30°，60°，90°，150°

【解析】试题分析：（1）连接BC，AD交于一点，则根据正方形的对角线相等的性质，OA=OB=OC=OD且AC⊥BD，可以得△OAB≌△0BC≌△OCD≌△OAD；

（2）分情况讨论即可；

（3）该等腰三角形的顶角为∠AOB=90°

试题解析： (1)连接BC，AD，BC、AD交于O点，

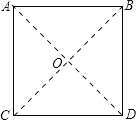
则OA=OB=OC=OD，

且∠AOB=∠BOC=∠COD=∠DOA，

∴△OAB≌△0BC≌△OCD≌△OAD，

故对角线交点O即为所求O点；

(2) 5个，分两种情况讨论：

第一种：等腰三角形一正方形的四条边为底边.因为等腰三角形的顶点必在底边的垂直平分线上，而AB、CD的垂直平分线和AD、BC的垂直平分线只有一个交点，即中点，所以O为中点；

第二种：等腰三角形以正方形的四条边为腰，如图所示，

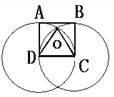
AD=OD，BC=DO，AO=BO，同理，这样的点有4个；

(3)第一种情况时，所有顶角度数都为90°，

第二种情况时，如图所示：△DOC为等边三角形，顶角为60°，所以相邻的两个顶角∠ADO=∠BCO=30°，所以第四个等边三角形顶角∠AOB=360°-60°-150°=150°.

关闭