
【题目】如图,矩形纸片ABCD,长AD=9cm,宽AB=3 cm,将其折叠,使点D与点B重合,那么折叠后DE的长和折痕EF的长分别为_______和__________.

【答案】 5cm ![]() cm
cm
【解析】试题解析:过点F作FH⊥AD交AD于点H,如图:
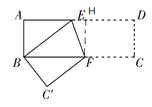
∵四边形EFCD和四边形EF C′B完全重合,
∴ED=BE.
∵ED=BE,DE=AD-AE=9-AE,
∴BE=9-AE,
∵在Rt△ABE中AB=3cm,BE=9-AE,
∴(9-AE)2=32+AE2,
∴AE=4cm.
∵AE=4cm,AD=9cm,
∴DE=5cm,
∵四边形EFCD和四边形EF C′B完全重合,
∴BC′=DC=3cm,C′F=CF,
∴C′F=BC-BF=9-BF,
∵在Rt△BFC′中,BC′=3cm,C′F=9-BF,
∴(9-BF)2+32=BF2,
∴BF=5cm.
∵BF=5cm,AE=4cm,
∴EH=1cm.
∵在Rt△EFH中,HF=3cm,EH=1cm,
∴EF=![]() (cm).
(cm).


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线y=﹣![]() x+b过点D,与线段AB相交于点F,求点F的坐标;
x+b过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF、OE,探究∠AOF与∠EOC的数量关系,并证明;
(4)若点P是x轴上的动点,点Q是(1)中的反比例函数在第一象限图象上的动点,且使得△PDQ是以PQ为斜边的等腰直角三角形,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
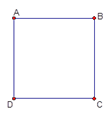
【题目】如图,四边形ABCD是一个正方形.
⑴请你在平面内找到一个点O,并连接OA、OB、OC、OD使得到△OAB、△BOC、△COD、△OAD都是等腰三角形.
⑵这样的点,你能找到多少个?
⑶试写出你找到的等腰三角形的顶角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饭店在2014年春节年夜饭的预定工作中,第一天预定了a桌,第二天预定的桌数比第一天多了4桌,则这两天该饭店一共预定了 桌年夜饭(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断题,对的画“√”错的画“×”
(1)对角线互相垂直的四边形是菱形(______)
(2)一条对角线垂直另一条对角线的四边形是菱形(_____)
(3)对角线互相垂直且平分的四边形是菱形(_____)
(4)对角线相等的四边形是菱形(_____)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com