
 如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.
如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC. 分析 构造以AE为直径的圆G,作圆G的直径MF,连接NF、BP.由题意可知∠EMA+∠ENA=180°,则点A、M、E、N共圆,由MN=MFsin∠MFN,AE=MF,∠MAN=∠MFN,可知MN=AEsin∠BAC,故此可得到AE=$\frac{MN}{sin∠BAC}$.由∠C=∠P,∠BAD=∠CAE可知△APB∽△ACE,从而得到$\frac{AB}{AE}=\frac{AP}{AC}$,故此可证明AP•MN=AB•AC•sin∠BAC.
解答 解:如图所示,构造以AE为直径的圆G,作圆G的直径MF,连接NF、BP.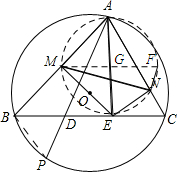
∵EM⊥AB,EN⊥AC,
∴∠EMA=∠ENA=90°.
∴∠EMA+∠ENA=180°.
点A、M、E、N共圆.
∵∠AME=90°,
∴AE是圆G的直径.
∵MF是圆G的直径,
∴∠MNF=90°.
∴MN=MFsin∠MFN.
∵AE=MF,∠MAN=∠MFN,
∴MN=AEsin∠BAC.
∴AE=$\frac{MN}{sin∠BAC}$.
∵∠C=∠P,∠BAD=∠CAE,
∴△APB∽△ACE.
∴$\frac{AB}{AE}=\frac{AP}{AC}$.
∴AP•AE=AB•AC.
∴AP•$\frac{MN}{sin∠BAC}$=AB•AC.
∴AP•MN=AB•AC•sin∠BAC.
点评 本题主要考查的圆周角定理、相似三角形的性质和判定、锐角三角函数的定义、四点共圆,证得AE=$\frac{MN}{sin∠BAC}$是解题的关键.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
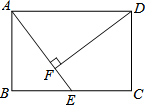 如图,在矩形ABCD中,E是BC边的中点,DF⊥AE,垂足为F.
如图,在矩形ABCD中,E是BC边的中点,DF⊥AE,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
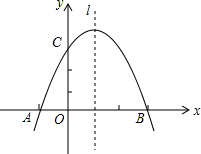 已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到.
已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
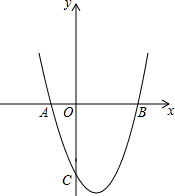 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
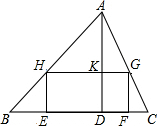 如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求四边形EFGH的面积.
如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求四边形EFGH的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,它正在播放动画片 | |
| B. | 播下一颗种子,种子一定会发芽 | |
| C. | 买100张中奖率为1%的彩票一定会中奖 | |
| D. | 太阳从东方升起 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com