
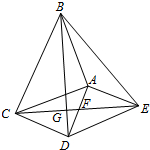
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
|
|


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
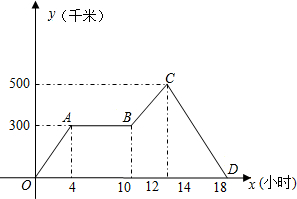 王老师从学校乘汽车去城里开会,4小时后,汽车出现故障,修理一段时间后继续走,又过了3个小时到达开会地点,而此时接到紧急通知,立马乘快客赶回学校.根据图中信息填空:
王老师从学校乘汽车去城里开会,4小时后,汽车出现故障,修理一段时间后继续走,又过了3个小时到达开会地点,而此时接到紧急通知,立马乘快客赶回学校.根据图中信息填空:查看答案和解析>>
科目:初中数学 来源: 题型:
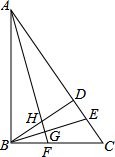 如图,在Rt△ABC中,∠ABC=90°,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.若∠BAC=30°,则
如图,在Rt△ABC中,∠ABC=90°,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.若∠BAC=30°,则| FC |
| HD |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com