
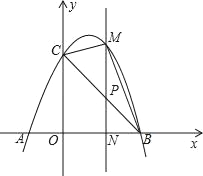
【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
【答案】(1)A(﹣1,0),B(3,0),C(0,3);(2)3+![]() ;(3)Q1(1,
;(3)Q1(1, ![]() ),Q2(1,
),Q2(1, ![]() ),Q3(1,﹣
),Q3(1,﹣![]() ),Q4(1,
),Q4(1, ![]() ).
).
【解析】试题分析:(1)依据抛物线的解析式直接求得C的坐标,令y=0解方程即可求得A、B点的坐标;
(2)求出△BCM面积的表达式,这是一个二次函数,求出其取最大值的条件;然后利用勾股定理求出△BPN的周长;
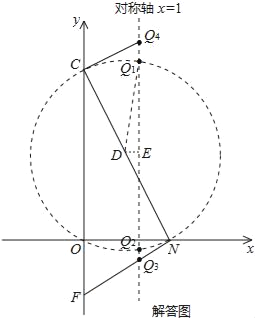
(3)如解答图,△CNQ为直角三角形,分三种情况:①点Q为直角顶点;②点N为直角顶点;③点C为直角顶点进行解答.
试题解析:(1)由抛物线的解析式y=﹣x2+2x+3,
∴C(0,3),
令y=0,﹣x2+2x+3=0,解得x=3或x=﹣1;
∴A(﹣1,0),B(3,0).
(2)设直线BC的解析式为:y=kx+b,则有:
![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为:y=﹣x+3.
设P(x,﹣x+3),则M(x,﹣x2+2x+3),
∴PM=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x.
∴S△BCM=S△PMC+S△PMB=![]() PM(xP﹣xC)+
PM(xP﹣xC)+![]() PM(xB﹣xP)=
PM(xB﹣xP)=![]() PM(xB﹣xC)=
PM(xB﹣xC)=![]() PM.
PM.
∴S△BCM=![]() (﹣x2+3x)=﹣
(﹣x2+3x)=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() .
.
∴当x=![]() 时,△BCM的面积最大.
时,△BCM的面积最大.
此时P![]() ,
, ![]() ),∴PN=ON=
),∴PN=ON=![]() ,
,
∴BN=OB﹣ON=3﹣![]() =
=![]() .
.
在Rt△BPN中,由勾股定理得:PB=![]() .
.
C△BCN=BN+PN+PB=3+![]() .
.
∴当△BCM的面积最大时,△BPN的周长为3+![]() .
.
(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴抛物线的对称轴为直线x=1.
在Rt△CNO中,OC=3,ON=![]() ,由勾股定理得:CN=
,由勾股定理得:CN=![]() .
.
设点D为CN中点,则D(![]() ,
, ![]() ),CD=ND=
),CD=ND=![]() .
.
如解答图,△CNQ为直角三角形,
①若点Q为直角顶点.
作Rt△CNO的外接圆⊙D,与对称轴交于Q1、Q2两点,由圆周角定理可知,Q1、Q2两点符合题意.
连接Q1D,则Q1D=CD=ND=![]() .
.
过点D(![]() ,
, ![]() )作对称轴的垂线,垂足为E,
)作对称轴的垂线,垂足为E,
则E(1, ![]() ),Q1E=Q2E,DE=1﹣
),Q1E=Q2E,DE=1﹣![]() =
=![]() .
.
在Rt△Q1DE中,由勾股定理得:
Q1E=![]() =
=![]() .
.
∴Q1(1, ![]() ),Q2(1,
),Q2(1, ![]() );
);
②若点N为直角顶点.
过点N作NF⊥CN,交对称轴于点Q3,交y轴于点F.
易证Rt△NFO∽Rt△CNO,则![]() ,即
,即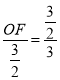 ,解得OF=
,解得OF=![]() .
.
∴F(0,﹣![]() ),又∵N(
),又∵N(![]() ,0),
,0),
∴可求得直线FN的解析式为:y=![]() x﹣
x﹣![]() .
.
当x=1时,y=﹣![]() ,
,
∴Q3(1,﹣ ![]() );
);
③当点C为直角顶点时.
过点C作Q4C⊥CN,交对称轴于点Q4.
∵Q4C∥FN,∴可设直线Q4C的解析式为:y=![]() x+b,
x+b,
∵点C(0,3)在该直线上,∴b=3.
∴直线Q4C的解析式为:y=![]() x+3,
x+3,
当x=1时,y=![]() ,
,
∴Q4(1, ![]() ).
).
综上所述,满足条件的点Q有4个,
其坐标分别为:Q1(1, ![]() ),Q2(1,
),Q2(1, ![]() ),Q3(1,﹣
),Q3(1,﹣![]() ),Q4(1,
),Q4(1, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=40![]() 厘米,∠CED=60°.
厘米,∠CED=60°.
(1)求垂直支架CD的长度;
(2)求水箱半径OD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
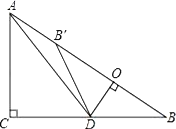
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
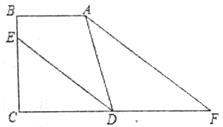
【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.求证:∠DAF=∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市从不同学校随机抽取100名初中生对“使用数学教辅用书的册数”进行调查,统计结果如下:
册数 | 0 | 1 | 2 | 3 |
人数 | 10 | 20 | 30 | 40 |
关于这组数据,下列说法正确的是( )
A.众数是2册B.中位数是2册
C.平均数是3册D.方差是1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 三点在数轴上,点
三点在数轴上,点![]() 表示的数是
表示的数是![]() ,从点
,从点![]() 出发向右平移7个单位长度得到点
出发向右平移7个单位长度得到点![]() 。
。
(1)求出点![]() 表示的数,画一条数轴并在数轴上标出点
表示的数,画一条数轴并在数轴上标出点![]() 和点
和点![]() ;
;
(2)若此数轴在一张纸上,将纸沿某一条直线对折,此时![]() 点与表示数
点与表示数![]() 的点刚好重合,折痕与数轴有一个交点
的点刚好重合,折痕与数轴有一个交点![]() ,求点
,求点![]() 表示的数的相反数(原卷无此问);
表示的数的相反数(原卷无此问);
(3)在数轴上有一点![]() ,点
,点![]() 到点
到点![]() 和点
和点![]() 的距离之和为11,求点
的距离之和为11,求点![]() 所表示的数;
所表示的数;
(4)![]() 从初始位置分别以1单位长度
从初始位置分别以1单位长度![]() 和2单位长度
和2单位长度![]() 的速度同时向左运动,是否存在
的速度同时向左运动,是否存在![]() 的值,使
的值,使![]() 秒后点
秒后点![]() 到
到![]() 的距离与点
的距离与点![]() 到原点距离相等?若存在请求出
到原点距离相等?若存在请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;
若直线![]() 上有
上有![]() 个点,一共有________条线段;
个点,一共有________条线段;

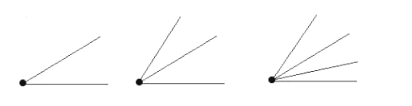
(2)有公共顶点的![]() 条射线可以组成_____个小于平角的角;
条射线可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
有公共顶点的![]() 条射线最多可以组成_____个小于平角的角;
条射线最多可以组成_____个小于平角的角;
(3)你学过的知识里还有满足类似规律的吗?试看写一个.
查看答案和解析>>
科目:初中数学 来源: 题型:
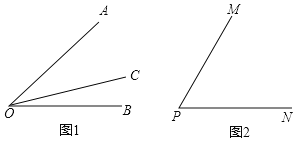
【题目】如图①,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图②,若![]() ,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为________.
,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com