
【题目】二次函数![]() 为常数,
为常数,![]() 中的
中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
x | -1 | 0 | 3 |
y | n | -3 | -3 |
当![]() 时,下列结论中一定正确的是________(填序号即可)
时,下列结论中一定正确的是________(填序号即可)
①![]() ;②当
;②当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大;③
值的增大而增大;③![]() ;④当
;④当![]() 时,关于
时,关于![]() 的一元二次方程
的一元二次方程![]() 的解是
的解是![]() ,
,![]() .
.
【答案】①②④
【解析】
①根据表格数据得到对称轴为![]() ,c=-3﹤0,又n﹥0知a﹥0,即可得出答案;
,c=-3﹤0,又n﹥0知a﹥0,即可得出答案;
②根据二次函数的性质即可解答;
③根据二次函数的性质,结合图象即可解答;
④利用待定系数法求出a、b、c,代入解一元二次方程即可解答.
由表格数据知,二次函数的对称轴为![]() ,且c=-3﹤0,
,且c=-3﹤0,
∵n﹥0,∴a﹥0,
∵对称轴![]() ﹥0,
﹥0,
∴b﹤0即 bc﹥0,故①正确;
∵a﹥0,对称轴为![]() ,
,
∴当x﹥![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大,
值的增大而增大,
∴当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大,
值的增大而增大,
故②正确;
③由对称轴![]() 得:b=-3a,
得:b=-3a,
∴![]()
∵当x=-1时,y=n,
∴n=a+3a-3=4a-3,
∴n﹤4a,故③错误;
④当n=1时,将(-1,1),(0,-3),(3,-3)代入函数解析式中,得:
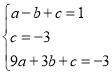 ,
,
解得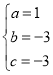 ,
,
∴关于x的一元二次方程为![]() ,解得
,解得![]() ,
,![]() ,
,
故④正确,
故答案是:①②④


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长是6,∠A=60°,E是AD的中点,F是AB边上一个动点,EG=EF且∠GEF=60°,则GB+GC的最小值是_____
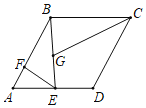
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在开展读书交流活动中,全体师生积极捐书,为了解所捐书籍的种类,对部分书籍进行了抽样调查,李老师根据调查数据绘制了如下不完整的统计图.请你根据统计回答下面问题:
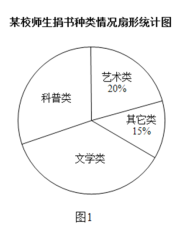

(1)本次抽样调查的书籍有多少本?请补全条形统计图;
(2)求出图1中表示文学类书籍的扇形圆心角度数;
(3)本次活动师生共捐书1200本,请估计有多少本科普类图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
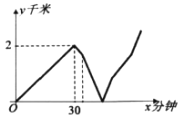
【题目】周末小明匀速步行赶往学校参加学校组织的植树活动,小明从家出发30分钟后,忽然想起没有带植树工具,于是马上掉头往回走行走速度比之前提高了1千米/时(仍保持匀速步行),同时小明打电话给爸爸,请爸爸帮他把植树工具送过来,从小明开始打电话到爸爸出门一共用了4分钟,爸爸的行走速度与此时小明的行走速度相同,两人相遇后,小明立即赶往学校,爸爸则转身回家,两人速度均保持不变,爸爸在回家途中用了10分钟吃早餐,然后立即回家,当爸爸到家时小明刚好到达学校.爸爸和小明相距的路程y(千米)与小明从家出发的时间x(分钟)之间的关系如图所示,求今天早上小明从家到学校途中行走的总路程是________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
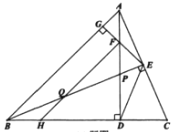
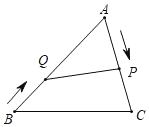
【题目】如图,在![]() 中,
中,![]() ,两条高AD,BE交于点P.过点E作
,两条高AD,BE交于点P.过点E作![]() ,垂足为G,交AD于点F,过点F作
,垂足为G,交AD于点F,过点F作![]() ,交BC于点H,交BE交于点Q,连接DE.
,交BC于点H,交BE交于点Q,连接DE.
(1)若![]() ,
,![]() ,求DE的长
,求DE的长
(2)若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过![]() 和
和![]() 两点的抛物线
两点的抛物线![]() 交
交![]() 轴于
轴于![]() 两点,
两点,![]() 是抛物线上一动点,平行于
是抛物线上一动点,平行于![]() 轴的直线
轴的直线![]() 经过点
经过点![]() .
.
(1)求抛物线的解析式;
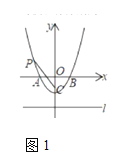
(2)如图1,![]() 轴上有点
轴上有点![]() 连接
连接![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.![]() .小明在探究
.小明在探究![]() 的值的过程中,是这样思考的:当
的值的过程中,是这样思考的:当![]() 是抛物线的顶点时,计算
是抛物线的顶点时,计算![]() 的值;当
的值;当![]() 不是抛物线的顶点时,猜想
不是抛物线的顶点时,猜想![]() 是一个定值.请你直接写出
是一个定值.请你直接写出![]() 的值,并证明小明的猜想.
的值,并证明小明的猜想.
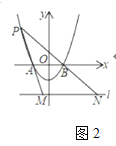
(3)如图2,点![]() 在第二象限,分别连接
在第二象限,分别连接![]() 、
、![]() ,并延长交直线
,并延长交直线![]() 于
于![]() 两点.若
两点.若![]() 两点的横坐标分别为
两点的横坐标分别为![]() ,试探究
,试探究![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16cm,AC=12cm,动点P、Q分别以每秒2cm和1cm的速度同时开始运动,其中点P从点A出发,沿AC边一直移到点C为止,点Q从点B出发沿BA边一直移到点A为止,(点P到达点C后,点Q继续运动)
(1)请直接用含t的代数式表示AP的长和AQ的长,并写出定义域.
(2)当t等于何值时,△APQ与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《![]() 年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分
年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分![]() 分),社区管理员随机从有
分),社区管理员随机从有![]() 人的某小区抽取若干名人员的答卷成绩,并对他们的成绩(单位:分)统计整理后绘制了一幅不完整的统计表(如图所示)
人的某小区抽取若干名人员的答卷成绩,并对他们的成绩(单位:分)统计整理后绘制了一幅不完整的统计表(如图所示)
等级 | 成绩( | 频数 | 频率 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
合计 |
|
| |
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() =___,
=___,![]() =_____;
=_____;
(2)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
(3)该社区有![]() 名男管理员和
名男管理员和![]() 名女管理员,现从中随机挑选
名女管理员,现从中随机挑选![]() 名管理员参加“社区防控”宣传活动,请用树状图法或列表法求出恰好选中“
名管理员参加“社区防控”宣传活动,请用树状图法或列表法求出恰好选中“![]() 男
男![]() 女”的概率.
女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点![]() 和
和![]() ,给出如下定义:
,给出如下定义:
如果 ,那么称点
,那么称点![]() 为点
为点![]() 的“伴随点”.
的“伴随点”.
例如:点![]() 的“伴随点”为点
的“伴随点”为点![]() ;点
;点![]() 的“伴随点”为点
的“伴随点”为点![]() .
.
(1)直接写出点![]() 的“伴随点”
的“伴随点”![]() 的坐标.
的坐标.
(2)点![]() 在函数
在函数![]() 的图象上,若其“伴随点”
的图象上,若其“伴随点”![]() 的纵坐标为2,求函数
的纵坐标为2,求函数![]() 的解析式.
的解析式.
(3)点![]() 在函数
在函数![]() 的图象上,且点
的图象上,且点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的“伴随点”为
的“伴随点”为![]() .若点
.若点![]() 在第一象限,且
在第一象限,且![]() ,求此时“伴随点”
,求此时“伴随点”![]() 的横坐标.
的横坐标.
(4)点![]() 在函数
在函数![]() 的图象上,若其“伴随点”
的图象上,若其“伴随点”![]() 的纵坐标
的纵坐标![]() 的最大值为
的最大值为![]() ,直接写出实数
,直接写出实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com