
【题目】某家电销售商场电冰箱的销售价为每台1600元,空调的销售价为每台1400元,每台电冰箱的进价比每台空调的进价多300元,商场用9000元购进电冰箱的数量与用7200元购进空调数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售利润为Y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于16200元,请分析合理的方案共有多少种?
(3)实际进货时,厂家对电冰箱出厂价下调K(0<K<150)元,若商场保持这两种家电的售价不变,请你根据以上信息及(2)中条件,设计出使这100台家电销售总利润最大的进货方案.
【答案】(1)每台空调的进价为1200元,每台电冰箱的进价为1500元;(2)共有5种方案;
(3)当100<k<150时,购进电冰箱38台,空调62台,总利润最大;当0<k<100时,购进电冰箱34台,空调66台,总利润最大,当k=100时,无论采取哪种方案,y1恒为20000元.
【解析】
(1)用“用9000元购进电冰箱的数量与用7200元购进空调数量相等”建立方程即可;(2)建立不等式组求出x的范围,代入即可得出结论;(3)建立y1=(k﹣100)x+20000,分三种情况讨论即可.
(1)设每台空调的进价为m元,则每台电冰箱的进价(m+300)元,
由题意得,![]() ,
,
∴m=1200,
经检验,m=1200是原分式方程的解,也符合题意,
∴m+300=1500元,
答:每台空调的进价为1200元,每台电冰箱的进价为1500元;
(2)由题意,y=(1600﹣1500)x+(1400﹣1200)(100﹣x)=﹣100x+20000,
∵![]() ,
,
∴33![]() ≤x≤38,
≤x≤38,
∵x为正整数,
∴x=34,35,36,37,38,
即:共有5种方案;
(3)设厂家对电冰箱出厂价下调k(0<k<150)元后,这100台家电的销售总利润为y1元,
∴y1=(1600﹣1500+k)x+(1400﹣1200)(100﹣x)=(k﹣100)x+20000,
当100<k<150时,y1随x的最大而增大,
∴x=38时,y1取得最大值,
即:购进电冰箱38台,空调62台,总利润最大,
当0<k<100时,y1随x的最大而减小,
∴x=34时,y1取得最大值,
即:购进电冰箱34台,空调66台,总利润最大,
当k=100时,无论采取哪种方案,y1恒为20000元.


科目:初中数学 来源: 题型:
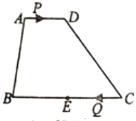
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 以每秒1个单位长度的速度从
以每秒1个单位长度的速度从![]() 点出发,沿
点出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒2个单位长度的速度从点
同时以每秒2个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,点
运动,点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.当运动时间
也随之停止运动.当运动时间![]() ______秒时,以点
______秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
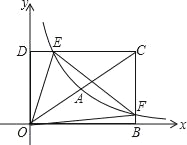
【题目】如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
(1)求反比例函数的解析式;
(2)求△OEF的面积;
(3)设直线EF的解析式为y=k2x+b,请结合图象直接写出不等式k2x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
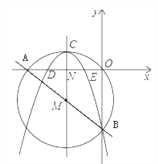
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.
(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
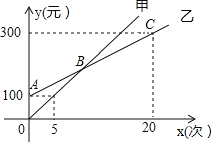
【题目】随着春节临近,某儿童游乐场推出了甲、乙两种消费卡,设消费次数为![]() 时,所需费用为
时,所需费用为![]() 元,且
元,且![]() 与
与![]() 的函数关系如图所示. 根据图中信息,解答下列问题;
的函数关系如图所示. 根据图中信息,解答下列问题;
(1)分别求出选择这两种卡消费时,![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)求出![]() 点坐标.
点坐标.
(3)洋洋爸爸准备![]() 元钱用于洋洋在该游乐场消费,请问选择哪种消费卡划算?
元钱用于洋洋在该游乐场消费,请问选择哪种消费卡划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
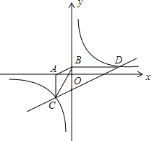
【题目】如图,已知双曲线![]() 经过点
经过点![]() ,点
,点![]() 是双曲线第三象限分支上的动点,过点
是双曲线第三象限分支上的动点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
![]() 求
求![]() 的值;
的值;
![]() 若
若![]() 的面积为
的面积为![]() ,
,
①若直线![]() 的解析式为
的解析式为![]() ,求
,求![]() 、
、![]() 的值;
的值;
②根据图象,直接写出![]() 时
时![]() 的取值范围;
的取值范围;
③判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
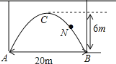
【题目】一拱形隧道的轮廓是抛物线如图,拱高![]() ,跨度
,跨度![]() .
.
![]() 建立适当的直角坐标系,求拱形隧道的抛物线关系式;
建立适当的直角坐标系,求拱形隧道的抛物线关系式;
![]() 拱形隧道下地平面是双向行车道(正中间是一条宽
拱形隧道下地平面是双向行车道(正中间是一条宽![]() 的隔离带),其中的一条行车道能否并排行驶宽
的隔离带),其中的一条行车道能否并排行驶宽![]() ,高
,高![]() 的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com