
【题目】如图,ABCD中,点E,F在对角线BD上,且BE=DF,求证: 
(1)AE=CF;
(2)四边形AECF是平行四边形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
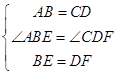 ,
,
∴△ABE≌△DCF(SAS).
∴AE=CF.
(2)证明:∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
【解析】(1)根据平行四边形的性质可得AB=CD,AB∥CD,然后可证明∠ABE=∠CDF,再利用SAS来判定△ABE≌△DCF,从而得出AE=CF.(2)首先根据全等三角形的性质可得∠AEB=∠CFD,根据等角的补角相等可得∠AEF=∠CFE,然后证明AE∥CF,从而可得四边形AECF是平行四边形.
【考点精析】关于本题考查的平行四边形的判定与性质,需要了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能得出正确答案.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】市移动通讯公司开设了两种通讯业务: “全球通” 使用者先缴50元月基础费, 然后每通话1分钟, 再付电话费0.4元; “神州行” 不缴月基础费, 每通话1分钟, 付话费0.6元(这里均指市内通话). 若一个月内通话x分钟, 两种通讯方式的费用分别为y1元和y2元.
(1)写出y1、y2与x之间的函数关系式;
(2)一个月内通话多少分钟, 两种通讯方式的费用相同?
(3)若某人预计一个月内使用话费200元, 则应选择哪种通讯方式较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(m ,n)在函数y x2的图象上,当-1 ≤ m ≤2时,则n的取值范围是( )
A.1 ≤ n ≤4B.0≤ n ≤4C.0≤ n ≤1D.-1≤ n ≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图象向上平移m(m>0)个单位再向右平移2个单位,则平移以后的二次函数的解析式为( )
A.y=(x+2)2﹣mB.y=(x+2)2+mC.y=(x+m)2+2D.y=(x﹣2)2+m
查看答案和解析>>
科目:初中数学 来源: 题型:
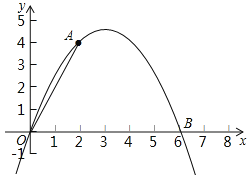
【题目】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y1=2x与双曲线y2= ![]() 的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<﹣1.”你同意他的观点吗? 答: . 理由是 .
的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<﹣1.”你同意他的观点吗? 答: . 理由是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com