
小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图13所示,樱桃单价w(单位:元/ kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.
樱桃单价w与上市时间x的关系
| x(天) | 1 | a | 9 | 11 | 13 | … |
| w(元/kg) | 32 | 32 | 24 | 20 | 16 | … |
(1)120kg;(2)当0≤x≤12时,y=10x;当12≤x≤20时,y=-15x+300;(3)5;(4)第12天的销售金额不是最多的.
解析试题分析:(1)根据函数图象的最高点的纵坐标解答;
(2)分0≤x≤12和12≤x≤20两段,利用待定系数法求一次函数解析式解答;
(3)利用待定系数法求一次函数解析式求出W与x的关系式,再求出W=32时的自变量的值即为a;
(4)求出x=12和10时的销售金额,比较即可判断.
(1)日销售量的最大值是120 kg;
(2)①当0≤x≤12时,函数图象过原点和(12,120)两点,
设日销售量y与上市时间x的函数解析式为y=kx,
由待定系数法得,120=12k,∴k=10,
即日销售量y与上市时间x的函数解析式为y=10x;
②当12≤x≤20时,函数图象过(20,0)和(12,120)两点,
设日销售量y与上市时间x的函数解析式为y=kx+b,
由待定系数法得,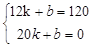 ,解得
,解得 ,
,
即日销售量y与上市时间x的函数解析式为y=-15x+300;
(3)设第a天之后,樱桃单价w与上市时间x的函数解析式为w=kx+b,
由待定系数法得,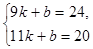 ,解得
,解得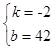 ,
,
即樱桃单价w与上市时间x的函数解析式为w=-2x+42,
当w=32时,x=5,所以a的值为5.
(4)第12天的销售金额不是最多的.
当x=12时,日销售量y=120千克,樱桃单价w=18元,销售金额为18×120=2160元;
当x=10时,日销售量y=100千克,樱桃单价w=22元,销售金额为22×100=2200元;
∵2200>2160,
∴第12天的销售金额不是最多的.
考点:一次函数的应用.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD= .延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.
.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.
(1)求点C的坐标;
(2)若点D在反比例函数y= (k>0)的图象上,求反比例函数的解析式.
(k>0)的图象上,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲乙两组工人同时开始加工某种零件,乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)之间函数图象如图所示.
(1)求数量y与时间x之间函数关系式.
(2)求乙组加工零件总量a值.
(3)甲乙两组加工出的零件合在一起装箱,每够300件装一箱,装箱时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20 km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2 (km), y1、y2 与x的函数关系如图所示.
(1)求y2与x的函数关系式;
(2)若两人在出发时都配备了通话距离为3km的对讲机,求甲、乙两人在骑行过程中可以用对讲机通话的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,反比例函数 与一次函数
与一次函数 的图象交于A(3,1)、B(m,-3)两点.
的图象交于A(3,1)、B(m,-3)两点.
(1)求反比例函数 与一次函数
与一次函数 的解析式.
的解析式.
(2)若点P是直线 上一点,且OP=
上一点,且OP= OA,请直接写出点P的坐标.
OA,请直接写出点P的坐标.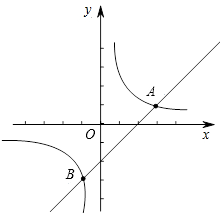
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,点A( ,0),点B(0,2),点C是线段OA的中点.
,0),点B(0,2),点C是线段OA的中点.
(1)点P是直线AB上的一个动点,当PC+PO的值最小时,
①画出符合要求的点P(保留作图痕迹);
②求出点P的坐标及PC+PO的最小值;
(2)当经过点O、C的抛物线y=ax2+bx+c与直线AB只有一个公共点时,求a的值并指出这个公共点所在象限.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,在平行四边形ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数y=kx+1(k≠0)与反比例函数y= (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地.如果是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.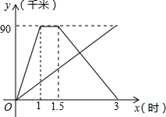
(1)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com