
【题目】如图,二次函数y=ax2+bx+c的图象的顶点C的坐标为(0,﹣2),交x轴于A、B两点,其中A(﹣1,0),直线l:x=m(m>1)与x轴交于D.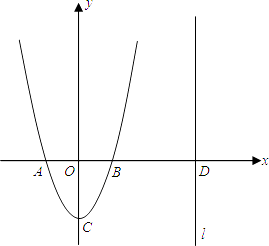
(1)求二次函数的解析式和B的坐标;
(2)在直线l上找点P(P在第一象限),使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似,求点P的坐标(用含m的代数式表示);
(3)在(2)成立的条件下,在抛物线上是否存在第一象限内的点Q,使△BPQ是以P为直角顶点的等腰直角三角形?如果存在,请求出点Q的坐标;如果不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=ax2+bx+c的顶点坐标为C(0,﹣2),
∴b=0,c=﹣2;
∵y=ax2+bx+c过点A(﹣1,0),
∴0=a+0﹣2,a=2,
∴抛物线的解析式为y=2x2﹣2.
当y=0时,2x2﹣2=0,
解得x=±1,
∴点B的坐标为(1,0)
(2)
解:设P(m,n).
∵∠PDB=∠BOC=90°,
∴当以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似时,分两种情况:
① 若△OCB∽△DBP,则 ![]() ,
,
即 ![]() =
= ![]() ,
,
解得n= ![]() .
.
由对称性可知,在x轴上方和下方均有一点满足条件,
∴此时点P坐标为(m, ![]() )或(m,
)或(m, ![]() ),
),
∵点P在第一象限,
∴点P的坐标为(m, ![]() )
)
②若△OCB∽△DPB,则 ![]() ,
,
即 ![]() =
= ![]() ,
,
解得n=2m﹣2.
由对称性可知,在x轴上方和下方均有一点满足条件,
∴此时点P坐标为(m,2m﹣2)或(m,2﹣2m),
∵P在第一象限,m>1,
∴点P的坐标为(m,2m﹣2)
综上所述,满足条件的点P的坐标为:(m, ![]() ),(m,2m﹣2)
),(m,2m﹣2)
(3)
解:方法一:
假设在抛物线上存在第一象限内的点Q(x,2x2﹣2),使△BPQ是以P为直角顶点的等腰直角三角形.
如图,过点Q作QE⊥l于点E.
∵∠DBP+∠BPD=90°,∠QPE+∠BPD=90°,
∴∠DBP=∠QPE.
在△DBP与△EPQ中,
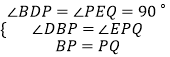 ,
,
∴△DBP≌△EPQ,
∴BD=PE,DP=EQ.
分两种情况:
①当P(m, ![]() )时,
)时,
∵B(1,0),D(m,0),E(m,2x2﹣2),
∴ 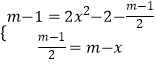 ,
,
解得 ![]() ,
, 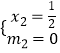 (均不合题意舍去);
(均不合题意舍去);
②当P(m,2(m﹣1))时,
∵B(1,0),D(m,0),E(m,2x2﹣2),
∴ ![]() ,
,
解得 ![]() ,
, 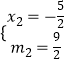 (均不合题意舍去);
(均不合题意舍去);
综上所述,不存在满足条件的点Q.
方法二:
若在第一象限内存在点Q,
①∵B(1,0),P(m, ![]() ),
),
点Q可视为点B绕点P顺时针旋转90°而成,
将点P平移至原点,得P′(0,0),则点B′(1﹣m, ![]() ),
),
将点B′顺时针旋转90°,则点Q′( ![]() ,m﹣1),
,m﹣1),
将点P′平移回P(m, ![]() ),则点Q′平移后即为点Q,
),则点Q′平移后即为点Q,
∴Q( ![]() ,
, ![]() ),
),
将点Q代入抛物线得:m2﹣m=0,
∴m1=1,m2=0,
∴Q1(1,0),Q2(0,﹣ ![]() )(均不合题意舍去),
)(均不合题意舍去),
②∵B(1,0),P(m,2m﹣2),
同理可得Q(2﹣m,3m﹣3),
将点Q代入抛物线得:3m﹣3=2(2﹣m)2﹣2,
∴2m2﹣11m+9=0,
∴m1=1,m2= ![]() ,
,
∴Q1(1,0),Q2(﹣ ![]() ,
, ![]() )(均不合题意舍去)
)(均不合题意舍去)
综上所述,不存在满足条件的点Q.
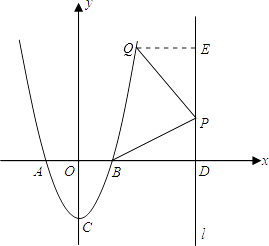
【解析】(1)由于抛物线的顶点C的坐标为(0,﹣2),所以抛物线的对称轴为y轴,且与y轴交点的纵坐标为﹣2,即b=0,c=﹣2,再将A(﹣1,0)代入y=ax2+bx+c,求出a的值,由此确定该抛物线的解析式,然后令y=0,解一元二次方程求出x的值即可得到点B的坐标;(2)设P点坐标为(m,n).由于∠PDB=∠BOC=90°,则D与O对应,所以当以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似时,分两种情况讨论:①△OCB∽△DBP;②△OCB∽△DPB.根据相似三角形对应边成比例,得出n与m的关系式,进而可得到点P的坐标;(3)假设在抛物线上存在第一象限内的点Q(x,2x2﹣2),使△BPQ是以P为直角顶点的等腰直角三角形.过点Q作QE⊥l于点E.利用AAS易证△DBP≌△EPQ,得出BD=PE,DP=EQ.再分两种情况讨论:①P(m, ![]() );②P(m,2(m﹣1)).都根据BD=PE,DP=EQ列出方程组,求出x与m的值,再结合条件x>0且m>1即可判断不存在第一象限内的点Q,使△BPQ是以P为直角顶点的等腰直角三角形.
);②P(m,2(m﹣1)).都根据BD=PE,DP=EQ列出方程组,求出x与m的值,再结合条件x>0且m>1即可判断不存在第一象限内的点Q,使△BPQ是以P为直角顶点的等腰直角三角形.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( ) 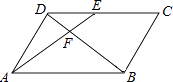
A.2:5
B.2:3
C.3:5
D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC中,OA=2,AB=4,双曲线 ![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.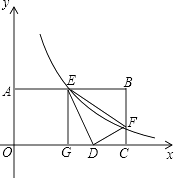
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y= ![]() x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
①PO2=PAPB;
②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;
③当k=- ![]() 时,BP2=BOBA;
时,BP2=BOBA;
④△PAB面积的最小值为 ![]() .
.
其中正确的是 . (写出所有正确说法的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上不与A、D重合的两点,连接MO、NO,并分别延长交BC边于M′、N′两点,则图中的全等三角形有_____对.
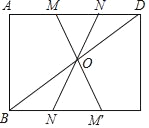
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个圆,一只电子跳蚤在标有数字的五个点上跳跃.若它停在奇数点上时,则一次沿顺时针方向跳两个点;若停在偶数点上时,则下一次沿逆时针方向跳一个点.若这只跳蚤从1这点开始跳,则经过2019次跳后它所停在的点对应的数为( )
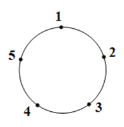
A. 1 B. 2 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com