
【题目】在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y= ![]() x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
①PO2=PAPB;
②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;
③当k=- ![]() 时,BP2=BOBA;
时,BP2=BOBA;
④△PAB面积的最小值为 ![]() .
.
其中正确的是 . (写出所有正确说法的序号)
【答案】③④
【解析】解:设A(m,km),B(n,kn),其中m<0,n>0.
联立y= ![]() x2﹣2与y=kx得:
x2﹣2与y=kx得: ![]() x2﹣2=kx,即x2﹣3kx﹣6=0,
x2﹣2=kx,即x2﹣3kx﹣6=0,
∴m+n=3k,mn=﹣6.
设直线PA的解析式为y=ax+b,将P(0,﹣4),A(m,km)代入得:![]() ,解得a=
,解得a= ![]() ,b=﹣4,
,b=﹣4,
∴y=( ![]() )x﹣4.
)x﹣4.
令y=0,得x= ![]() ,
,
∴直线PA与x轴的交点坐标为( ![]() ,0).
,0).
同理可得,直线PB的解析式为y=( ![]() )x﹣4,直线PB与x轴交点坐标为(
)x﹣4,直线PB与x轴交点坐标为( ![]() ,0).
,0).
∵ ![]() +
+ ![]() =
= ![]() =
= ![]() =0,
=0,
∴直线PA、PB与x轴的交点关于y轴对称,即直线PA、PB关于y轴对称.
1)说法①错误.理由如下:
如答图1所示,∵PA、PB关于y轴对称,
∴点A关于y轴的对称点A′落在PB上.
连接OA′,则OA=OA′,∠POA=∠POA′.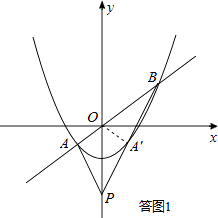
假设结论:PO2=PAPB成立,即PO2=PA′PB,
∴ ![]() ,
,
又∵∠BPO=∠BPO,
∴△POA′∽△PBO,
∴∠POA′=∠PBO,
∴∠AOP=∠PBO.
而∠AOP是△PBO的外角,
∴∠AOP>∠PBO,矛盾,
∴说法①错误.
2)说法②错误.理由如下:
易知: ![]() =﹣
=﹣ ![]() ,
,
∴OB=﹣ ![]() OA.
OA.
由对称可知,PO为△APB的角平分线,
∴ ![]() ,
,
∴PB=﹣ ![]() PA.
PA.
∴(PA+AO)(PB﹣BO)=(PA+AO)[﹣ ![]() PA﹣(﹣
PA﹣(﹣ ![]() OA)]=﹣
OA)]=﹣ ![]() (PA+AO)(PA﹣OA)=﹣
(PA+AO)(PA﹣OA)=﹣ ![]() (PA2﹣AO2).
(PA2﹣AO2).
如答图2所示,过点A作AD⊥y轴于点D,则OD=﹣km,PD=4+km.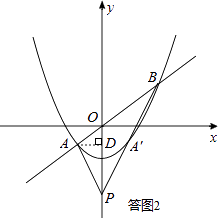
∴PA2﹣AO2=(PD2+AD2)﹣(OD2+AD2)=PD2﹣OD2=(4+km)2﹣(﹣km)2=8km+16,
∵m+n=3k,∴k= ![]() (m+n),
(m+n),
∴PA2﹣AO2=8 ![]() (m+n)m+16=
(m+n)m+16= ![]() m2+
m2+ ![]() mn+16=
mn+16= ![]() m2+
m2+ ![]() ×(﹣6)+16=
×(﹣6)+16= ![]() m2 .
m2 .
∴(PA+AO)(PB﹣BO)=﹣ ![]() (PA2﹣AO2)=﹣
(PA2﹣AO2)=﹣ ![]()
![]() m2=﹣
m2=﹣ ![]() mn=﹣
mn=﹣ ![]() ×(﹣6)=16.
×(﹣6)=16.
即:(PA+AO)(PB﹣BO)为定值,所以说法②错误.
3)说法③正确.理由如下:
当k= ![]() 时,联立方程组:
时,联立方程组:  ,得A(
,得A( ![]() ,2),B(
,2),B( ![]() ,﹣1),
,﹣1),
∴BP2=12,BOBA=2×6=12,
∴BP2=BOBA,故说法③正确.
4)说法④正确.理由如下:
S△PAB=S△PAO+S△PBO= ![]() OP(﹣m)+
OP(﹣m)+ ![]() OPn=
OPn= ![]() OP(n﹣m)=2(n﹣m)=2
OP(n﹣m)=2(n﹣m)=2 ![]() =2
=2 ![]() ,
,
∴当k=0时,△PAB面积有最小值,最小值为 ![]() =
= ![]() .
.
故说法④正确.
综上所述,正确的说法是:③④.
所以答案是:③④.
【考点精析】本题主要考查了根与系数的关系的相关知识点,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知:关于x的方程mx2-3(m+1)x+2m+3=0(m≠0).
(1)若方程有两个相等的实数根,求m的值;
(2)求此方程的两个根(若所求方程的根不是常数,就用含m的式子表示);
(3)若m为整数,当m取何值时方程的两个根均为正整数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现用等式AM=(i,j)表示正奇数M是第i组第j个数(从左往右数),如A7=(2,3),则A2013=( )
A.(45,77)
B.(45,39)
C.(32,46)
D.(32,23)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象的顶点C的坐标为(0,﹣2),交x轴于A、B两点,其中A(﹣1,0),直线l:x=m(m>1)与x轴交于D.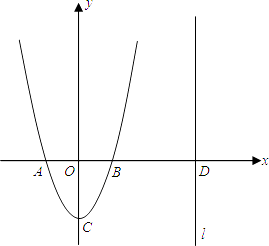
(1)求二次函数的解析式和B的坐标;
(2)在直线l上找点P(P在第一象限),使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似,求点P的坐标(用含m的代数式表示);
(3)在(2)成立的条件下,在抛物线上是否存在第一象限内的点Q,使△BPQ是以P为直角顶点的等腰直角三角形?如果存在,请求出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013成都)若正整数n使得在计算n+(n+1)+(n+2)的过程中,各数位均不产生进位现象,则称n为“本位数”.例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物体从P点运动到Q点所用时间为7秒,其运动速度v(米每秒)关于时间t(秒)的函数关系如图所示.某学习小组经过探究发现:该物体前进3秒运动的路程在数值上等于矩形AODB的面积.由物理学知识还可知:该物体前t(3<t≤7)秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和. 根据以上信息,完成下列问题: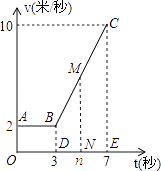
(1)当3<t≤7时,用含t的式子表示v;
(2)分别求该物体在0≤t≤3和3<t≤7时,运动的路程s(米)关于时间t(秒)的函数关系式;并求该物体从P点运动到Q总路程的 ![]() 时所用的时间.
时所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC. 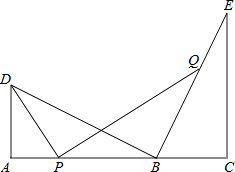
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q; (i)当点P与A、B两点不重合时,求 ![]() 的值;
的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜公司收购蔬菜260吨,准备加工后上市销售.该公司的加工能力是:每天精加工8吨或粗加工20吨.现计划在22天内完成加工任务,且尽可能多的精加工,该公司应安排几天精加工,几天粗加工,才能按期完成任务?如果每吨蔬菜粗加工后的利润是1500元,精加工后的利润为3000元,那么该公司出售这些加工后的蔬菜共可获利多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O,根据下列条件,求出∠BOC的度数.
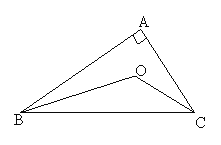
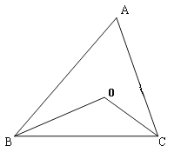
(1)已知∠ABC+∠ACB=100°,则∠BOC= .
(2)已知∠A=90°,求∠BOC的度数.
(3)从上述计算中,你能发现∠BOC与∠A的关系吗?请直接写出∠B0C与∠A的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com