
【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现用等式AM=(i,j)表示正奇数M是第i组第j个数(从左往右数),如A7=(2,3),则A2013=( )
A.(45,77)
B.(45,39)
C.(32,46)
D.(32,23)
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】为方便市民出行,减轻城市中心交通压力,某市正在修建贯穿全城南北、东西的地铁1,2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元,且1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线、2号线每千米的平均造价分别是多少亿元;
(2)除1,2号线外,该市规划到2019年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC中,OA=2,AB=4,双曲线 ![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.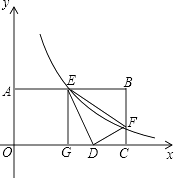
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y= ![]() x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
①PO2=PAPB;
②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;
③当k=- ![]() 时,BP2=BOBA;
时,BP2=BOBA;
④△PAB面积的最小值为 ![]() .
.
其中正确的是 . (写出所有正确说法的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算机系统对文件的管理通常采用树形目录结构,方式如图,在一个根目录下建立若干子目录(这里称第一层目录),每个子目录又可作为父目录,向下继续建立其子目录(这里称第二层目录),依次进行,可创建多层目录.现在一根目录下建立了四层目录,并且每一个父目录下的子目录的个数都相同,都等于根目录下目录的个数.已知第三层目录共有343个,求这一根目录下的所有目录的个数.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com