
����Ŀ��Ϊ����������У�����������Ľ�ͨѹ����ij���������ᴩȫ���ϱ��������ĵ���1��2���ߣ���֪������1����24ǧ��2����22ǧ����Ͷ��265��Ԫ����1����ÿǧ��ƽ����۱�2����ÿǧ��ƽ����۶�0.5��Ԫ��
(1)��1���ߡ�2����ÿǧ��ƽ����۷ֱ��Ƕ�����Ԫ��
(2)��1��2�����⣬���й滮��2019�껹Ҫ�ٽ�91.8ǧ�ĵ�����������Ԥ�㣬��91.8ǧ��������ÿǧ��ƽ�������1����ÿǧ��ƽ����۵�1.2��������Ͷ�ʶ�����Ԫ��
���𰸡�(1)1���ߡ�2����ÿǧ��ƽ����۷ֱ���6��Ԫ��5.5��Ԫ;(2) 660.96��Ԫ��
��������
����1���ߣ�2����ÿǧ��ƽ����۷ֱ���x��Ԫ��y��Ԫ�����ݡ�������1����24ǧ��2����22ǧ����Ͷ��265��Ԫ����1����ÿǧ��ƽ����۱�2���ߵ�ƽ����۶�0.5��Ԫ���ֱ�ó���ʽ������ɣ�
���ݣ�1��������ó���91.8ǧ�ĵ���������ÿǧ����ۣ�����������ɣ�
�⣺(1)��1���ߡ�2����ÿǧ��ƽ����۷ֱ���x��Ԫ��y��Ԫ��
�������![]()
���![]()
��1���ߡ�2����ÿǧ��ƽ����۷ֱ���6��Ԫ��5.5��Ԫ��
(2)91.8��6��1.2��660.96(��Ԫ)��
�𣺻���Ͷ��660.96��Ԫ��


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���忼�ڼ���������1����Ŀ����о�С��Ա��꼶530��ѧ�����������������е��飬��������ͼ��ʾ��ͳ��ͼ������1����50�ˣ���ע��30������Ϊ��꣬����50�֣�����ͳ��ͼ������������⣺ 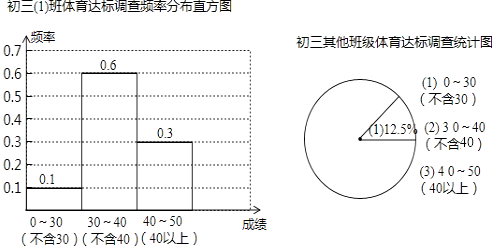
��1��������1����ѧ����������ʺͱ��꼶�������ѧ����������ʸ��Ƕ��٣�
��2������������1����������༶ѧ���������Գɼ���30����40�ֵ���120�ˣ��벹ȫ����ͳ��ͼ����ע������ͼ�з���������Ӧ��Բ�ĽǵĶ�����
��3�����Ҫ��ȫ�꼶ѧ������������ʲ�����90%�������ڱ��ε����У����꼶ȫ��ѧ��������������Ƿ����Ҫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=x2��1��x����������ڵ�A����y���ڵ�B����������������ƽ��4����λ��������y2 �� �����������ཻ�ڵ�C��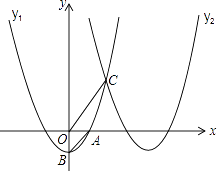
��1����ֱ��д��������y2�Ľ���ʽ��
��2������P��x����һ���㣬�������CPA=��OBA�������������������P�����ꣻ
��3���ڵ���������������y2�ϣ��Ƿ���ڵ�Q��ʹ�á�QOC��OC���ϵĸ�h�����ֵ�������ڣ��������Q�����꼰h�����ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ���mx2-3��m+1��x+2m+3=0��m��0����
��1����������������ȵ�ʵ��������m��ֵ��
��2����˷��̵��������������̵ĸ����dz��������ú�m��ʽ�ӱ�ʾ����
��3����mΪ��������mȡ��ֵʱ���̵���������Ϊ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
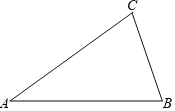
����Ŀ����ͼ����ABC���ܳ�Ϊ20������AB=8��
��1����ֱ�ߺ�Բ���� AB �Ĵ�ֱƽ���� DE �� AC �ڵ� E������Ϊ D������ EB����������ͼ�ۼ�����Ҫ��д������
��2���ڣ�1������ AB �Ĵ�ֱƽ���� DE �����CBE ���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���C����ͼ��ʽ������һ�����У���A=60�㣬��D=30�㣻��E=��B=45�㣩��
��1��������DCE=45�㣬���ACB�Ķ���Ϊ������
������ACB=140�㣬���DCE�Ķ�����
��2���ɣ�1�������ACB���DCE��������ϵ����˵�����ɣ�
��3������ACE��180���ҵ�E��ֱ��AC���Ϸ�ʱ�����������dz��Ƿ����һ�����ƽ�У������ڣ���ֱ��д����ACE�Ƕ����п��ܵ�ֵ������˵�����ɣ����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
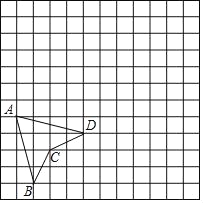
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳�Ϊ1���ı���ABCD�Ķ��㶼�ڸ���ϣ�
(1)�ڷ���ֽ�Ͻ���ƽ��ֱ������ϵ��ʹ�ı���ABCD�Ķ���A��C������ֱ�Ϊ(��5����1)��(��3����3)����д����D�����ꣻ
(2)��(1)����������ϵ�У������ı���ABCD����x��ĶԳ�ͼ��A1B1C1D1����д����B�Ķ�Ӧ��B1�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������С�������У��������¹��ɷ��飺��1������3��5��7������9��11��13��15��17������19��21��23��25��27��29��31�����������õ�ʽAM=��i��j����ʾ������M�ǵ�i���j����������������������A7=��2��3������A2013=�� ��
A.��45��77��
B.��45��39��
C.��32��46��
D.��32��23��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B���߶�AC�ϣ���D��E��ACͬ�࣬��A=��C=90�㣬BD��BE��AD=BC�� 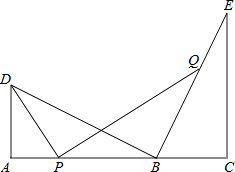
��1����֤��AC=AD+CE��
��2����AD=3��CE=5����PΪ�߶�AB�ϵĶ��㣬����DP����PQ��DP����ֱ��BE�ڵ�Q�� ��i������P��A��B���㲻�غ�ʱ���� ![]() ��ֵ��
��ֵ��
��ii������P��A���˶���AC���е�ʱ�����߶�DQ���е���������·�����߶Σ�������ֱ��д�����������д�������̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com