
����Ŀ����ͼ��������y1=x2��1��x����������ڵ�A����y���ڵ�B����������������ƽ��4����λ��������y2 �� �����������ཻ�ڵ�C��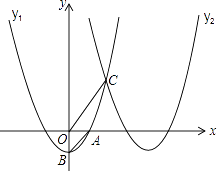
��1����ֱ��д��������y2�Ľ���ʽ��
��2������P��x����һ���㣬�������CPA=��OBA�������������������P�����ꣻ
��3���ڵ���������������y2�ϣ��Ƿ���ڵ�Q��ʹ�á�QOC��OC���ϵĸ�h�����ֵ�������ڣ��������Q�����꼰h�����ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺������y1=x2��1����ƽ��4����λ�Ķ�������Ϊ��4����1����
���ԣ�������y2�Ľ���ʽΪy2=��x��4��2��1
��2��
�⣺x=0ʱ��y=��1��
y=0ʱ��x2��1=0�����x1=1��x2=��1��
���ԣ���A��1��0����B��0����1����
���OBA=45�㣬
���� ![]() ��
��
��� ![]() ��
��
���C��������2��3����
�ߡ�CPA=��OBA��
���P�ڵ�A�����ʱ������Ϊ����1��0����
�ڵ�A���ұ�ʱ������Ϊ��5��0����
���ԣ���P������Ϊ����1��0����5��0��
��3��
�⣺���ڣ�
�ߵ�C��2��3����
��ֱ��OC�Ľ���ʽΪy= ![]() x��
x��
����OCƽ�е�ֱ��y= ![]() x+b��
x+b��
����  ��
��
����y�ã�2x2��19x+30��2b=0��
����=0��������������ȵ�ʵ����ʱ����QOC��OC���ϵĸ�h�����ֵ��
��ʱx1=x2= ![]() ������
������ ![]() ��=
��= ![]() ��
��
��ʱy=�� ![]() ��4��2��1=��
��4��2��1=�� ![]() ��
��
����ڵ������ĵ�Q�� ![]() ����
���� ![]() ����ʹ�á�QOC��OC���ϵĸ�h�����ֵ��
����ʹ�á�QOC��OC���ϵĸ�h�����ֵ��
��ʱ��=192��4��2����30��2b��=0��
���b=�� ![]() ��
��
�����Q��OCƽ�е�ֱ�߽���ʽΪy= ![]() x��
x�� ![]() ��
��
��y=0���� ![]() x��
x�� ![]() =0�����x=
=0�����x= ![]() ��
��
��ֱ����x��Ľ���ΪE����E�� ![]() ��0����
��0����
����C��CD��x����D�����ݹ��ɶ�����OC= ![]() =
= ![]() ��
��
��sin��COD= ![]() =
= ![]() ��
��
���h���= ![]() ��
�� ![]() =
= ![]() ��
��

����������1��д��ƽ�ƺ�������ߵĶ������꣬Ȼ�����ö���ʽ����ʽд�����ɣ���2�����������߽���ʽ�����A��B�����꣬Ȼ�������OBA=45�㣬�������������߽���ʽ�������C�����꣬�ٸ��ݡ�CPA=��OBA�ֵ�P�ڵ�A����ߺ��ұ����������⣻��3�������ֱ��OC�Ľ���ʽΪy= ![]() x������OCƽ�е�ֱ��y=
x������OCƽ�е�ֱ��y= ![]() x+b����������y2��������y�õ�����x��һԪ���η��̣��ٸ�����OC�ľ������ʱ��������ֻ��һ������Ȼ�����ø����б�ʽ��=0��ʽ���b��ֵ���Ӷ��õ�ֱ�ߵĽ���ʽ���������x��Ľ���E�����꣬�õ�OE�ij��ȣ��ٹ���C��CD��x����D��Ȼ����ݡ�COD������ֵ��⼴�ɵõ�h��ֵ��
x+b����������y2��������y�õ�����x��һԪ���η��̣��ٸ�����OC�ľ������ʱ��������ֻ��һ������Ȼ�����ø����б�ʽ��=0��ʽ���b��ֵ���Ӷ��õ�ֱ�ߵĽ���ʽ���������x��Ľ���E�����꣬�õ�OE�ij��ȣ��ٹ���C��CD��x����D��Ȼ����ݡ�COD������ֵ��⼴�ɵõ�h��ֵ��
�����㾫�������ն��κ����������ǽ����ĸ�������Ҫ֪�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0����ͼ�����M����2�� ![]() ������������ΪN����1��
������������ΪN����1�� ![]() ��������x�ύ��A��B���㣬��y�ύ��C�㣮
��������x�ύ��A��B���㣬��y�ύ��C�㣮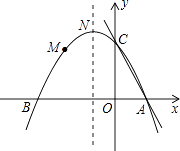
��1���������ߵĽ���ʽ��
��2����PΪ�����߶Գ����ϵĶ��㣬����PBCΪ����������ʱ�����P�����ꣻ
��3����ֱ��AC���Ƿ����һ��Q��ʹ��QBM���ܳ���С�������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�����A��C��D��������y=ax2+bx+c��a��0������x�����һ����ΪE������CE����A��B��D������ֱ�Ϊ����2��0������3��0������0��4����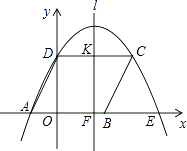
��1���������ߵĽ���ʽ��
��2����֪�����ߵĶԳ���l��x���ڵ�F�����߶�CD�ڵ�K����M��N�ֱ���ֱ��l��x���ϵĶ��㣬����MN�����߶�MNǡ�ñ�BC��ֱƽ��ʱ�����N�����ꣻ
��3�������㣨2���������£�����M��һ��ֱ�ߣ�ʹ֮���ı���AECD�������Ϊ3��4�������֣������ֱ�ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�����O�ں��й����У����ֵ���A������ƫ��60��ķ����ϣ�ͬʱ��������ƫ��30�㡢����������ƫ��45�㣩�������ֱַ����˿���B�ͺ���C��
��1����ֱ���ͼ���л�����ʾ����B�ͺ���C���������OB��OC����д��������
��2����ͼ����һ���洬D���ҡ�AOD�IJ�����������ǵ�3������ͼ���л�����ʾ�洬D���������OD�������洬D�ڻ���O�ķ�λ�ǣ�
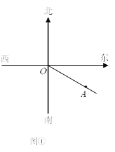
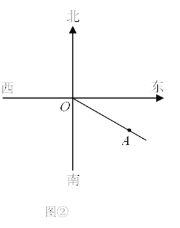
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�EΪCD��һ�㣬����AE��BD����AE��BD���ڵ�F��S��DEF��S��ABF=4��25����DE��EC=�� �� 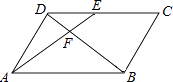
A.2��5
B.2��3
C.3��5
D.3��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������������վ������һ���ڽ������ߣ�������ÿ��8���Ӿ�ӭ�濪��һ����������ÿ��24���ִӱ�����һ���������������վ�����ļ��ʱ����ͬ���������ٶ���ͬ��������վ�����ļ��ʱ��Ϊ��������
A. 18���� B. 10���� C. 12���� D. 16����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����������У�����������Ľ�ͨѹ����ij���������ᴩȫ���ϱ��������ĵ���1��2���ߣ���֪������1����24ǧ��2����22ǧ����Ͷ��265��Ԫ����1����ÿǧ��ƽ����۱�2����ÿǧ��ƽ����۶�0.5��Ԫ��
(1)��1���ߡ�2����ÿǧ��ƽ����۷ֱ��Ƕ�����Ԫ��
(2)��1��2�����⣬���й滮��2019�껹Ҫ�ٽ�91.8ǧ�ĵ�����������Ԥ�㣬��91.8ǧ��������ÿǧ��ƽ�������1����ÿǧ��ƽ����۵�1.2��������Ͷ�ʶ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����OABC�У�OA=2��AB=4��˫���� ![]() ��k��0�����������AB��BC�ֱ���E��F��
��k��0�����������AB��BC�ֱ���E��F��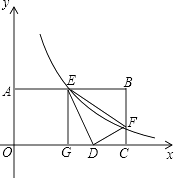
��1����E��AB���е㣬��F������ꣻ
��2��������BEF��ֱ��EF���ۣ�B������x���ϵ�D�㣬��EG��OC������ΪG��֤����EGD�ס�DCF������k��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com