
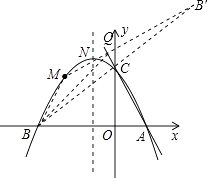
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2, ![]() ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1, ![]() ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.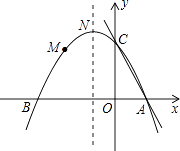
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.
【答案】
(1)
解:由抛物线顶点坐标为N(﹣1, ![]() ),可设其解析式为y=a(x+1)2+
),可设其解析式为y=a(x+1)2+ ![]() ,
,
将M(﹣2, ![]() )代入,得
)代入,得 ![]() =a(﹣2+1)2+
=a(﹣2+1)2+ ![]() ,
,
解得a=﹣ ![]() ,
,
故所求抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]()
(2)
解:∵y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ,
,
∴x=0时,y= ![]() ,
,
∴C(0, ![]() ).
).
y=0时,﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() =0,
=0,
解得x=1或x=﹣3,
∴A(1,0),B(﹣3,0),
∴BC= ![]() =2
=2 ![]() .
.
设P(﹣1,m),
当CP=CB时,有CP= ![]() =2
=2 ![]() ,解得m=
,解得m= ![]() ±
± ![]() ;
;
当BP=BC时,有BP= ![]() =2
=2 ![]() ,解得m=±2
,解得m=±2 ![]() ;
;
当PB=PC时, ![]() =
= ![]() ,解得m=0,
,解得m=0,
综上,当△PBC为等腰三角形时,点P的坐标为(﹣1, ![]() +
+ ![]() ),(﹣1,
),(﹣1, ![]() ﹣
﹣ ![]() ),(﹣1,2
),(﹣1,2 ![]() ),(﹣1,﹣2
),(﹣1,﹣2 ![]() ),(﹣1,0)
),(﹣1,0)
(3)
解:由(2)知BC=2 ![]() ,AC=2,AB=4,
,AC=2,AB=4,
所以BC2+AC2=AB2,即BC⊥AC.
连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,
∵B、B′关于直线AC对称,
∴QB=QB′,
∴QB+QM=QB′+QM=MB′,
所以此时△QBM的周长最小.
由B(﹣3,0),C(0, ![]() ),易得B′(3,2
),易得B′(3,2 ![]() ).
).
设直线MB′的解析式为y=kx+n,
将M(﹣2, ![]() ),B′(3,2
),B′(3,2 ![]() )代入,
)代入,
得 ![]() ,解得
,解得 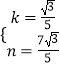 ,
,
即直线MB′的解析式为y= ![]() x+
x+ ![]() .
.
同理可求得直线AC的解析式为y=﹣ ![]() x+
x+ ![]() .
.
由 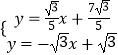 ,解得
,解得 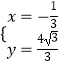 ,即Q(﹣
,即Q(﹣ ![]() ,
, ![]() ).
).
所以在直线AC上存在一点Q(﹣ ![]() ,
, ![]() ),使△QBM的周长最小.
),使△QBM的周长最小.
【解析】(1)先由抛物线的顶点坐标为N(﹣1, ![]() ),可设其解析式为y=a(x+1)2+
),可设其解析式为y=a(x+1)2+ ![]() ,再将M(﹣2,
,再将M(﹣2, ![]() )代入,得
)代入,得 ![]() =a(﹣2+1)2+
=a(﹣2+1)2+ ![]() ,解方程求出a的值即可得到抛物线的解析式;(2)先求出抛物线y=﹣
,解方程求出a的值即可得到抛物线的解析式;(2)先求出抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() 与x轴交点A、B,与y轴交点C的坐标,再根据勾股定理得到BC=
与x轴交点A、B,与y轴交点C的坐标,再根据勾股定理得到BC= ![]() =2
=2 ![]() .设P(﹣1,m),当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC;(3)先由勾股定理的逆定理得出BC⊥AC,连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,由轴对称的性质可知此时△QBM的周长最小,由B(﹣3,0),C(0,
.设P(﹣1,m),当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC;(3)先由勾股定理的逆定理得出BC⊥AC,连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,由轴对称的性质可知此时△QBM的周长最小,由B(﹣3,0),C(0, ![]() ),根据中点坐标公式求出B′(3,2
),根据中点坐标公式求出B′(3,2 ![]() ),再运用待定系数法求出直线MB′的解析式为y=
),再运用待定系数法求出直线MB′的解析式为y= ![]() x+
x+ ![]() ,直线AC的解析式为y=﹣
,直线AC的解析式为y=﹣ ![]() x+
x+ ![]() ,然后解方程组
,然后解方程组 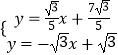 ,即可求出Q点的坐标.
,即可求出Q点的坐标.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x=2,则2|x|-1=3.以上命题是真命题的有( ).
A. ①②③④ B. ①④ C. ②④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若AD=6,AB=14,请求出CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
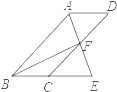
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体考在即,初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查,制作出如图所示的统计图,其中1班有50人.(注:30分以上为达标,满分50分)根据统计图,解答下面问题: 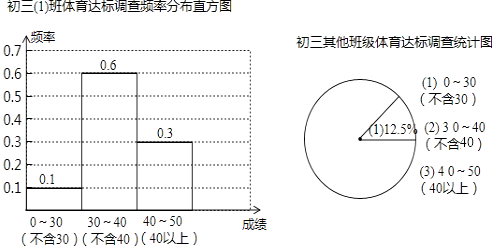
(1)初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少?
(2)若除初三(1)班外其余班级学生体育考试成绩在30﹣﹣40分的有120人,请补全扇形统计图;(注:请在图中分数段所对应的圆心角的度数)
(3)如果要求全年级学生的体育达标率不低于90%,试问在本次调查中,该年级全体学生的体育达标率是否符合要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=x2﹣1交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2 , 两条抛物线相交于点C.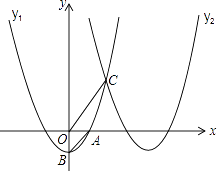
(1)请直接写出抛物线y2的解析式;
(2)若点P是x轴上一动点,且满足∠CPA=∠OBA,求出所有满足条件的P点坐标;
(3)在第四象限内抛物线y2上,是否存在点Q,使得△QOC中OC边上的高h有最大值?若存在,请求出点Q的坐标及h的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com