
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�����A��C��D��������y=ax2+bx+c��a��0������x�����һ����ΪE������CE����A��B��D������ֱ�Ϊ����2��0������3��0������0��4����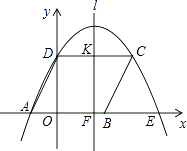
��1���������ߵĽ���ʽ��
��2����֪�����ߵĶԳ���l��x���ڵ�F�����߶�CD�ڵ�K����M��N�ֱ���ֱ��l��x���ϵĶ��㣬����MN�����߶�MNǡ�ñ�BC��ֱƽ��ʱ�����N�����ꣻ
��3�������㣨2���������£�����M��һ��ֱ�ߣ�ʹ֮���ı���AECD�������Ϊ3��4�������֣������ֱ�ߵĽ���ʽ��
���𰸡�
��1��
�⣺�ߵ�A��B��D������ֱ�Ϊ����2��0������3��0������0��4�������ı���ABCD��ƽ���ı��Σ�
��AB=CD=5��
���C��������5��4����
�߹���A��C��D��������y=ax2+bx+c��a��0����
�� 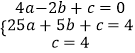 ��
��
��� 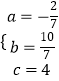 ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x+4
x+4
��2��
�⣺����BD���Գ�����G��
��Rt��OBD������BD=5��
��CD=BD�����DCB=��DBC��
�֡ߡ�DCB=��CBE��
���DBC=��CBE��
��G��GN��BC��H����x����N��
��֤GH=HN��
���G���M�غϣ�
��ֱ��BD�Ľ���ʽy=�� ![]() x+4
x+4
���������߿�֪�Գ��᷽��Ϊx= ![]() ��
��
���M�������� ![]() ��
�� ![]() ������GF=
������GF= ![]() ��BF=
��BF= ![]() ��
��
��BM= ![]() =
= ![]() ��
��
�֡�MN��BC��ֱƽ�֣�
��BM=BN= ![]() ��
��
���N�������� ![]() ��0��
��0��
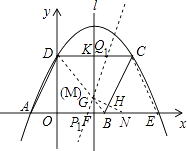
��3��
�⣺����M��ֱ�߽�x���ڵ�P1������CE��
�����ı���AECD�����Ϊ28���ı���ABCD�����Ϊ20��
�ɡ��ı���AECD�������Ϊ3��4����ֱ֪��P1M�����߶�CD�ཻ��
�轻��ΪQ1���ı���AP1Q1D�����ΪS1���ı���P1ECQ1�����ΪS2����P1������Ϊ��a��0����
�����P�ڶԳ������࣬��P1F= ![]() ��a��P1E=7��a��
��a��P1E=7��a��
�ɡ�MKQ1�ס�MFP1���� ![]() =
= ![]() ��
��
����Q1K=5P1F=5�� ![]() ��a����
��a����
��CQ1= ![]() ��5��
��5�� ![]() ��a��=5a��10��
��a��=5a��10��
��S2= ![]() ��5a��10+7��a����4=28��
��5a��10+7��a����4=28�� ![]() ��
��
��ã�a= ![]() ��
��
����P1�� ![]() ��0����M��
��0����M�� ![]() ��
�� ![]() ������ֱ��P1M�Ľ���ʽΪy=
������ֱ��P1M�Ľ���ʽΪy= ![]() x��6��
x��6��
����P�ڶԳ�����Ҳ࣬��ֱ��P2M�Ľ���ʽΪy=�� ![]() x+
x+ ![]()
����������1������ƽ���ı��ε����ʿ����C�����꣬�ɴ���ϵ����������������ߵĽ���ʽ����2������BD���Գ�����G����G��GN��BC��H����x����N�����ݴ���ϵ�����������ֱ��BD�Ľ���ʽ�����������߶Գ��ṫʽ����Գ��ᣬ�ɴ˼��������N�����ꣻ��3������M��ֱ�߽�x���ڵ�P1 �� �ֵ�P�ڶԳ������࣬��P�ڶԳ�����Ҳ࣬����������ۼ������ֱ�ߵĽ���ʽ��
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
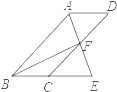
����Ŀ����ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E��
��1����֤��BE=CD��
��2������BF����BF��AE����BEA=60�㣬AB=4����ƽ���ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���忼�ڼ���������1����Ŀ����о�С��Ա��꼶530��ѧ�����������������е��飬��������ͼ��ʾ��ͳ��ͼ������1����50�ˣ���ע��30������Ϊ��꣬����50�֣�����ͳ��ͼ������������⣺ 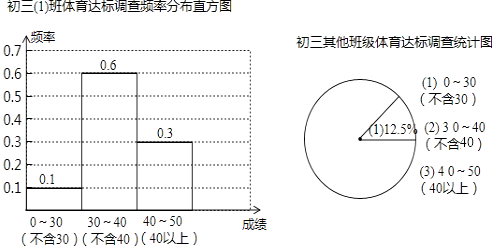
��1��������1����ѧ����������ʺͱ��꼶�������ѧ����������ʸ��Ƕ��٣�
��2������������1����������༶ѧ���������Գɼ���30����40�ֵ���120�ˣ��벹ȫ����ͳ��ͼ����ע������ͼ�з���������Ӧ��Բ�ĽǵĶ�����
��3�����Ҫ��ȫ�꼶ѧ������������ʲ�����90%�������ڱ��ε����У����꼶ȫ��ѧ��������������Ƿ����Ҫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l�ֱ���x�ᡢy�ύ��A��B���㣬��˫����y= ![]() ��a��0��x��0���ֱ���D��E���㣮
��a��0��x��0���ֱ���D��E���㣮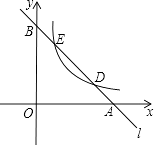
��1������D��������4��1������E��������1��4����
�ٷֱ����ֱ��l��˫���ߵĽ���ʽ��
������ֱ��l����ƽ��m��m��0������λ����mΪ��ֵʱ��ֱ��l��˫��������ֻ��һ�����㣿
��2�������A������Ϊ��a��0������B������Ϊ��0��b������DΪ�߶�AB��n�ȷֵ㣬��ֱ��д��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ��a��b������һ�����㡰��Ϊ��ab=a2+ab��2�����������⣺ ��13=2��
�ڷ���x1=0�ĸ�Ϊ��x1=��2��x2=1��
�۲���ʽ�� ![]() �Ľ⼯Ϊ����1��x��4��
�Ľ⼯Ϊ����1��x��4��
�ܵ㣨 ![]() ��
�� ![]() ���ں���y=x����1����ͼ���ϣ�
���ں���y=x����1����ͼ���ϣ�
������ȷ���ǣ� ��
A.�٢ڢۢ�
B.�٢�
C.�٢ڢ�
D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
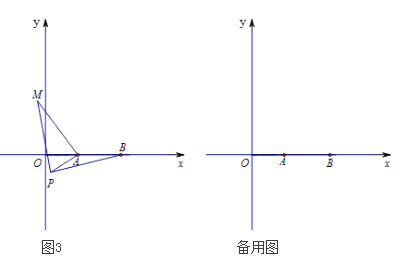
����Ŀ����1����ͼ1����AΪ�߶�BC��һ���㣬��BC=a��AB=b����գ�����Aλ���� ��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ�� �����ú�a��b��ʽ�ӱ�ʾ����
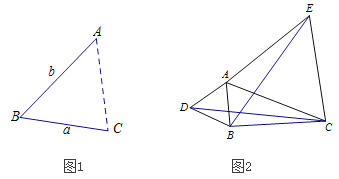
��2����ͼ2������AΪ�߶�BC��һ���㣬��BC=4��AB=2���ֱ���AB��ACΪ�ߣ����ȱ�![]() �͵ȱ�
�͵ȱ�![]() ������CD��BE.
������CD��BE.
��ͼ�����߶�BE��ȵ��߶����߶� ����˵�����ɣ�
��ֱ��д���߶�BE�������ֵΪ ��
��3����ͼ3����ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��5��0������PΪ�߶�AB��һ���㣬��PA=2��PM=PB����BPM=90�㣬��ֱ��д���߶�AM�������ֵΪ ������ʱ��P������Ϊ ������ʾ������ֱ�������ε����߳�a��b��c����a��b��c=1��1��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=x2��1��x����������ڵ�A����y���ڵ�B����������������ƽ��4����λ��������y2 �� �����������ཻ�ڵ�C��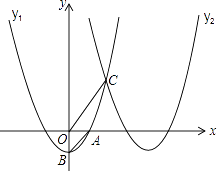
��1����ֱ��д��������y2�Ľ���ʽ��
��2������P��x����һ���㣬�������CPA=��OBA�������������������P�����ꣻ
��3���ڵ���������������y2�ϣ��Ƿ���ڵ�Q��ʹ�á�QOC��OC���ϵĸ�h�����ֵ�������ڣ��������Q�����꼰h�����ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
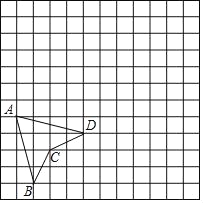
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳�Ϊ1���ı���ABCD�Ķ��㶼�ڸ���ϣ�
(1)�ڷ���ֽ�Ͻ���ƽ��ֱ������ϵ��ʹ�ı���ABCD�Ķ���A��C������ֱ�Ϊ(��5����1)��(��3����3)����д����D�����ꣻ
(2)��(1)����������ϵ�У������ı���ABCD����x��ĶԳ�ͼ��A1B1C1D1����д����B�Ķ�Ӧ��B1�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com