
【题目】如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y= ![]() (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.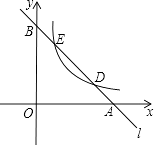
(1)若点D的坐标为(4,1),点E的坐标为(1,4):
①分别求出直线l与双曲线的解析式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
【答案】
(1)
解:①把D(4,1)代入y= ![]() 得a=1×4=4,
得a=1×4=4,
所以反比例函数解析式为y= ![]() (x>0);
(x>0);
设直线l的解析式为y=kx+t,
把D(4,1),E(1,4)代入得 ![]() ,
,
解得 ![]() .
.
所以直线l的解析式为y=﹣x+5;
②直线l向下平移m(m>0)个单位得到y=﹣x+5﹣m,
当方程组 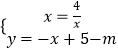 只有一组解时,直线l与双曲线有且只有一个交点,
只有一组解时,直线l与双曲线有且只有一个交点,
化为关于x的方程得x2+(m﹣5)x+4=0,
△=(m﹣5)2﹣4×4=0,解得m1=1,m2=9,
而m=9时,解得x=﹣2,故舍去,
所以当m=1时,直线l与双曲线有且只有一个交点
(2)
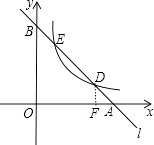
解:作DF⊥x轴,如图,
∵点D为线段AB的n等分点,
∴DA:AB=1:n,
∵DF∥OB,
∴△ADF∽△ABO,
∴ ![]() ,即
,即 ![]() ,
,
∴AF= ![]() ,DF=
,DF= ![]() ,
,
∴OF=a﹣ ![]() ,
,
∴D点坐标为(a﹣ ![]() ,
, ![]() ),
),
把D(a﹣ ![]() ,
, ![]() )代入y=
)代入y= ![]() 得(a﹣
得(a﹣ ![]() )
) ![]() =a,
=a,
解得b= ![]() .
.
【解析】(1)①运用待定系数法可分别得到直线l与双曲线的解析式;
②直线l向下平移m(m>0)个单位得到y=﹣x=5﹣m,根据题意得方程组 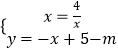 只有一组解时,化为关于x的方程得x2+(m﹣5)x+4=0,则△=(m﹣5)2﹣4×4=0,解得m1=1,m2=9,当m=9时,公共点不在第一象限,所以m=1;(2)作DF⊥x轴,由DF∥OB得到△ADF∽△ABO,根据相似比可得到AF=
只有一组解时,化为关于x的方程得x2+(m﹣5)x+4=0,则△=(m﹣5)2﹣4×4=0,解得m1=1,m2=9,当m=9时,公共点不在第一象限,所以m=1;(2)作DF⊥x轴,由DF∥OB得到△ADF∽△ABO,根据相似比可得到AF= ![]() ,DF=
,DF= ![]() ,则D点坐标为(a﹣
,则D点坐标为(a﹣ ![]() ,
, ![]() ),然后把D点坐标代入反比例函数解析式中即可得到b的值.
),然后把D点坐标代入反比例函数解析式中即可得到b的值.
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知不在同一条直线上的三点A,B,C.
(1)按下列要求作图(用尺规作图,不要求写做法,但要保留作图痕迹,并书写结论)
①分别作射线BA,线段AC;
②在线段BA的延长线上作AD=AC.
(2)若∠CAD比∠CAB大100°,则∠CAB的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如,图中三角形ABC是格点三角形,其中S=2,N=0,L=6;图中格点多边形DEFGHI所对应的S,N,L分别是 . 经探究发现,任意格点多边形的面积S可表示为S=aN+bL+c,其中a,b,c为常数,则当N=5,L=14时,S= . (用数值作答)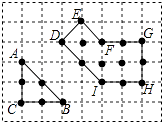
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A’B’C’,若它移动的距离AA’等于1cm,则两个三角形重叠部分的面积为____________cm2.
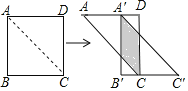
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,过点A、C、D作抛物线y=ax2+bx+c(a≠0),与x轴的另一交点为E,连结CE,点A、B、D的坐标分别为(﹣2,0)、(3,0)、(0,4).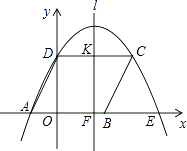
(1)求抛物线的解析式;
(2)已知抛物线的对称轴l交x轴于点F,交线段CD于点K,点M、N分别是直线l和x轴上的动点,连结MN,当线段MN恰好被BC垂直平分时,求点N的坐标;
(3)在满足(2)的条件下,过点M作一条直线,使之将四边形AECD的面积分为3:4的两部分,求出该直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:

(1)写出图2中所表示的数学等式 。
(2)根据整式乘法的运算法则,通过计算验证上述等式。
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
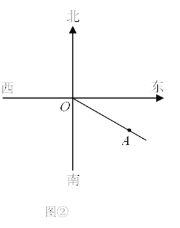
【题目】如图①,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
(1)请分别在图①中画出表示客轮B和海岛C方向的射线OB,OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,在图②中画出表示渔船D方向的射线OD,并求渔船D在货轮O的方位角.
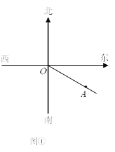
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)的图象与x轴交于A(x1 , 0)、B(x2 , 0)(x1<x2)两点,与y轴交于点C,x1 , x2是方程x2+4x﹣5=0的两根.
(1)若抛物线的顶点为D,求S△ABC:S△ACD的值;
(2)若∠ADC=90°,求二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com