
【题目】已知:关于x的方程mx2-3(m+1)x+2m+3=0(m≠0).
(1)若方程有两个相等的实数根,求m的值;
(2)求此方程的两个根(若所求方程的根不是常数,就用含m的式子表示);
(3)若m为整数,当m取何值时方程的两个根均为正整数?
【答案】(1)m1=m2=-3.(2)x1=1,x2=![]() .(3)当m取1、3或-3时,方程的两个根均为正整数.
.(3)当m取1、3或-3时,方程的两个根均为正整数.
【解析】
(1)根据方程的系数结合根的判别式△=0,即可得出关于m的一元二次方程,解之即可得出m的值;
(2)利用因式分解法解一元二次方程,即可得出结论;
(3)根据(2)的结论结合方程的两个根均为正整数,即可得出![]() 的值,解之即可得出m的值.
的值,解之即可得出m的值.
解:(1)∵方程有两个相等的实数根,
∴△=[-3(m+1)]2-4m(2m+3)=0,
∴(m+3)2=0,
∴m1=m2=-3.
(2)∵mx2-3(m+1)x+2m+3=0,即[mx-(2m+3)](x-1)=0,
解得:x1=1,x2=![]() .
.
(3)∵x1=1、x2=![]() =2+
=2+![]() 均为正整数,且m为整数,
均为正整数,且m为整数,
∴![]() =1、-1或3.
=1、-1或3.
当![]() =1时,m=3,
=1时,m=3,
当![]() =-1时,m=-3,
=-1时,m=-3,
当![]() =3时,m=1.
=3时,m=1.
∴当m取1、3或-3时,方程的两个根均为正整数.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60,得到△BAE,连接ED,若BC=5,BD=4,则有以下四个结论:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC。其中正确结论的序号是( )
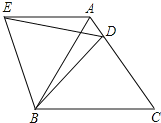
A. ②③④ B. ①③④ C. ①②④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( ) 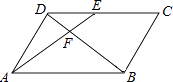
A.2:5
B.2:3
C.3:5
D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个公共汽车站相向发车,一人在街上行走,他发现每隔8分钟就迎面开来一辆公交车,每隔24分种从背后开来一辆公交车,如果车站发车的间隔时间相同,各车的速度相同,那两车站发车的间隔时间为( )
A. 18分钟 B. 10分钟 C. 12分钟 D. 16分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y= ![]() x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M10的坐标为 .
x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M10的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民出行,减轻城市中心交通压力,某市正在修建贯穿全城南北、东西的地铁1,2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元,且1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线、2号线每千米的平均造价分别是多少亿元;
(2)除1,2号线外,该市规划到2019年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y= ![]() x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
x2﹣2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
①PO2=PAPB;
②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;
③当k=- ![]() 时,BP2=BOBA;
时,BP2=BOBA;
④△PAB面积的最小值为 ![]() .
.
其中正确的是 . (写出所有正确说法的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com