
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
分析 先由m+n-p=0,得出m-p=-n,m+n=p,n-p=-m,再根据m($\frac{1}{n}$-$\frac{1}{p}$)+n($\frac{1}{m}$-$\frac{1}{p}$)-p($\frac{1}{m}$+$\frac{1}{n}$)=$\frac{m-p}{n}$+$\frac{n-p}{m}$-$\frac{m+n}{p}$代入化简即可.
解答 解:∵m+n-p=0,
∴m-p=-n,
m+n=p,
n-p=-m,
∴m($\frac{1}{n}$-$\frac{1}{p}$)+n($\frac{1}{m}$-$\frac{1}{p}$)-p($\frac{1}{m}$+$\frac{1}{n}$)=$\frac{m}{n}$-$\frac{m}{p}$+$\frac{n}{m}$-$\frac{n}{p}$-$\frac{p}{m}$-$\frac{p}{n}$=$\frac{m-p}{n}$+$\frac{n-p}{m}$-$\frac{m+n}{p}$=$\frac{-n}{n}$+$\frac{-m}{m}$-$\frac{p}{p}$=-1-1-1=-3;
故选:A.
点评 此题考查了分式的化简求值,用到的知识点是约分、分式的加减,关键是把原式变形为$\frac{-n}{n}$+$\frac{-m}{m}$-$\frac{p}{p}$.


科目:初中数学 来源: 题型:解答题
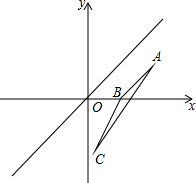 已知直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称.
已知直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
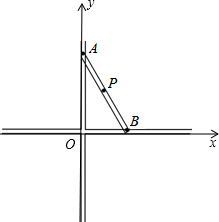 著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能分别在纵向滑槽内、横向滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.按如图所示建立平面直角坐标系.已知AB=10cm,
著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能分别在纵向滑槽内、横向滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.按如图所示建立平面直角坐标系.已知AB=10cm,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com