
 如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.
如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6. 分析 分两种情形①如图1中,当CB=CA′时,易知四边形BCA′M是菱形.②如图2中,当A′B=A′C时,易知MA′∥AC.分别求解即可.
解答 解:分两种情形①如图1中,当CB=CA′时,易知四边形BCA′M是菱形.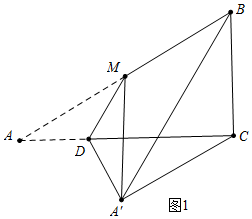
∴∠MA′C=∠ABC=60°,
∵∠MAD=∠MA′D=30°,'
∴∠CA′D=90°,
∵CA′∥AB,
∴∠A′CD=30°,
∴CD=2DA′=2AD,
在Rt△ABC中,∵∠A=30°,BC=6,
∴AC=6$\sqrt{3}$,AB=2BC=12,
∴AD=$\frac{1}{3}$AC=2$\sqrt{3}$.
②如图2中,当A′B=A′C时,易知MA′∥AC.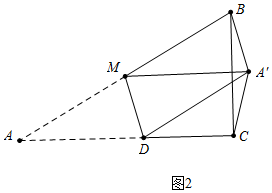
∴∠A′MD=∠ADM=∠AMD,
∴AM=AD,
∵AM=BM,AB=12,
∴AD=6.
故答案为2$\sqrt{3}$或6.
点评 本题考查翻折变换、等腰三角形的性质、直角三角形30度角的性质等知识,解题的关键是西合营4分类讨论的思想思考问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=$\frac{x}{2}$+$\frac{2}{x}$的图象和性质.| x | … | -5 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{29}{10}$ | -$\frac{5}{2}$ | -$\frac{13}{6}$ | -2 | -$\frac{5}{2}$ | -$\frac{17}{4}$ | $\frac{17}{4}$ | $\frac{5}{2}$ | 2 | m | $\frac{5}{2}$ | $\frac{29}{10}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
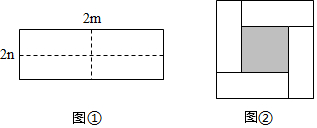
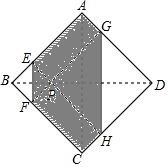 如图,正方形纸片ABCD的边长为2,翻折∠B、∠D.使两个直角的顶点重合于直线BD上一点P.EF与GH为折痕.若BP=$\frac{1}{4}$AC,则图中阴影部分的六边形AEFCHG的面积为$\frac{11}{4}$.
如图,正方形纸片ABCD的边长为2,翻折∠B、∠D.使两个直角的顶点重合于直线BD上一点P.EF与GH为折痕.若BP=$\frac{1}{4}$AC,则图中阴影部分的六边形AEFCHG的面积为$\frac{11}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
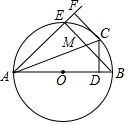 如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.
如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com