
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
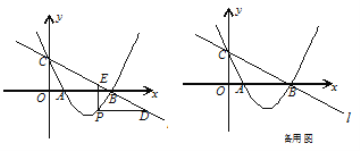
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
【答案】(1)抛物线的解析式为![]() (2)当
(2)当![]() 时,PD+PE的最大值是3(3)能,以A、B、P、F为顶点的四边形能构成平行四边形.此时点F的坐标为F(3,
时,PD+PE的最大值是3(3)能,以A、B、P、F为顶点的四边形能构成平行四边形.此时点F的坐标为F(3, ![]() )或F(1,
)或F(1, ![]() )
)
【解析】试题分析: (1)在![]() 中求出
中求出![]() 和
和![]() 时
时![]() 与
与![]() 的值可得点
的值可得点![]() 的坐标,根据点
的坐标,根据点![]() 坐标利用待定系数法可得抛物线解析式;
坐标利用待定系数法可得抛物线解析式;
(2)设P(![]() ,
, ![]() ),则D(
),则D(![]() ,
, ![]() ),
),
E(![]() ,
, ![]() ),用
),用![]() 表示出
表示出![]() ,配方即可求出最大值.
,配方即可求出最大值.
(3)令![]() ,求出点
,求出点![]() 坐标,求出
坐标,求出![]() 的值,然后分类讨论.
的值,然后分类讨论.
试题解析:
(1)∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,
轴分别交于点B、C,
∴B(2,0)、C(0,1),
∵B、C在抛物线解![]() 上,
上,
∴![]() ,
,
解得: 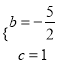 ,
,
∴抛物线的解析式为![]() .
.
(2)设P(![]() ,
, ![]() ),
),
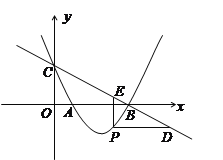
∵PD∥![]() 轴,PE∥
轴,PE∥![]() 轴,点D,E都在直线
轴,点D,E都在直线![]() 上,
上,
∴E(![]() ,
, ![]() ),D(
),D(![]() ,
, ![]() ),
),
∴PD+PE=![]() ,
,
![]() ,
,
![]() ,
,
∴当![]() 时,PD+PE的最大值是3.
时,PD+PE的最大值是3.
(3)能,理由如下:
由![]() ,令
,令![]() ,
,
解得: ![]() ,
, ![]() ,
,
∴A(![]() ,0),B(2,0),
,0),B(2,0),
∴![]() ,
,
若以A、B、P、F为顶点的四边形能构成平行四边形,
①当以AB为边时,则AB∥PF且AB=PF,
设P(![]() ,
, ![]() ),则F(
),则F(![]() ,
, ![]() ),
),
∴![]() ,
,
整理得: ![]() ,
,
解得: ![]() ,
, ![]() (与A重合,舍去),
(与A重合,舍去),
∴F(3, ![]() ),
),
②当以AB为对角线时,连接PF交AB于点G,则AG=BG,PG=FG,
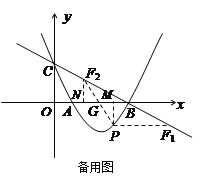
设G(m,0),
∵A(![]() ,0),B(2,0),
,0),B(2,0),
∴m-![]() =2-m,∴m=
=2-m,∴m=![]() ,
,
∴G(![]() ,0),
,0),
作PM⊥AB于点M,FN⊥AB于点N,则NG=MG,PM=FN,
设P(![]() ,
, ![]() ),则F(
),则F(![]() ,
, ![]() ),
),
∴![]() ,
,
整理得: ![]() ,
,
解得: ![]() ,
, ![]() (与A重合,舍去),
(与A重合,舍去),
∴F(1, ![]() ).
).
综上所述,以A、B、P、F为顶点的四边形能构成平行四边形.此时点F的坐标为F(3, ![]() )或F(1,
)或F(1, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】为了掌握某次数学模拟考试卷的命题质量与难度系数,命题教师选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
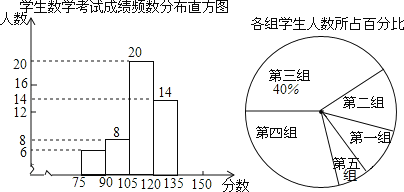
请将频数分布直方图补充完整;若老师找到第五组中一个学生的语文、数学、英语三科成绩,如表.老师将语文、数学、英语成绩按照3:5:2的比例给出这位同学的综合分数.求此同学的综合分数.
科目 | 语文 | 数学 | 英语 |
得分 | 120 | 146 | 140 |
查看答案和解析>>
科目:初中数学 来源: 题型:
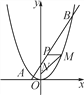
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
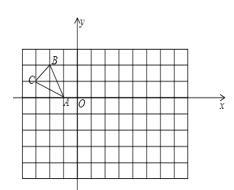
【题目】如图,在边长均为l的小正方形网格纸中,△ABC的顶点A、B、C均在格点上,O为直角坐标系的原点,点A(﹣1,0)在x轴上.
(1)以O为位似中心,将△ABC放大,使得放大后的△A1B1C1与△ABC的相似比为2:1,要求所画△A1B1C1与△ABC在原点两侧;
(2)分别写出B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … | -2 | -1 | 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中正确的是______.(填写序号)
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②函数
; ②函数![]() 的最大值为6;
的最大值为6;
③抛物线的对称轴是直线![]() ; ④在对称轴左侧,
; ④在对称轴左侧,![]() 随
随![]() 增大而增大.
增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
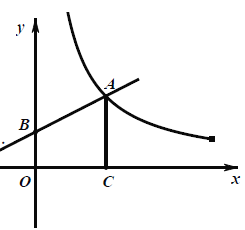
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 与一次函数
与一次函数![]() 在
在![]() 轴上方的图象的交点,过点
轴上方的图象的交点,过点![]() 作
作![]() 轴,垂足是点
轴,垂足是点![]() ,
,![]() .一次函数
.一次函数![]() 的图象与
的图象与![]() 轴的正半轴交于点
轴的正半轴交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若梯形![]() 的面积是3,求一次函数
的面积是3,求一次函数![]() 的解析式;
的解析式;
(3)结合这两个函数的完整图象:当![]() 时,写出
时,写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com