
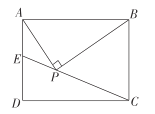
【题目】如图,在矩形ABCD中,![]() ,在矩形内有一点P,同时满足
,在矩形内有一点P,同时满足![]()
![]() ,延长CP交AD于点E,则
,延长CP交AD于点E,则![]() ______.
______.
【答案】![]()
【解析】
延长AP交CD于F,根据已知条件得到∠CPF+∠CPB=90°,根据矩形的性质得到∠DAB=∠ABC=90°,BC=AD=3,根据余角的性质得到∠EAP=∠ABP,推出AE=PE,根据勾股定理CD2+DE2=CE2即可求出AE的长,继而得到结论.
解:延长AP交CD于F,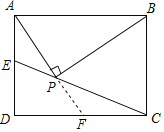
∵∠APB=90°,
∴∠FPB=90°,
∴∠CPF+∠CPB=90°,
∵四边形ABCD是矩形,
∴∠DAB=∠ABC=90°,BC=AD=3,
∴∠EAP+∠BAP=∠ABP+∠BAP=90°,
∴∠EAP=∠ABP,
∵CP=CB=3,
∴∠CPB=∠CBP,
∴∠CPF=∠ABP=∠EAP,
∵∠EPA=∠CPF,
∴∠EAP=∠APE,
∴AE=PE,
∵CD2+DE2=CE2,
∴42+(3-AE)2=(3+AE)2,
∴![]()
∴CE=3+![]() =
=![]()
故答案为:![]()


科目:初中数学 来源: 题型:
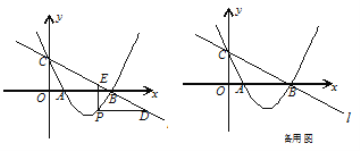
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
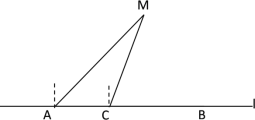
【题目】如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东45°方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上.
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东30°的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
(参考数据:sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,![]() ≈1.732.)
≈1.732.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 经过点A(-2,0),B(4,0)两点,与
经过点A(-2,0),B(4,0)两点,与![]() 轴交于点C,点D是抛物线上一个动点,设点D的横坐标为
轴交于点C,点D是抛物线上一个动点,设点D的横坐标为![]() .连接AC,BC,DB,DC,
.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若点M是![]() 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下 5 个项目可供选择:径赛项目:100m、200m、1000m(分别用 A1、A2、A3 表示);田赛项目:跳远,跳高(分别用 T1、T2 表示).
(1)该同学从 5 个项目中任选一个,恰好是田赛项目的概率 P 为 ;
(2)该同学从 5 个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率 P1,利用列表法或树状图加以说明;
(3)该同学从 5 个项目中任选两个,则两个项目都是径赛项目的概率 P2 为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
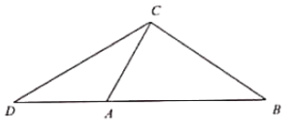
【题目】如图,已知在![]() 中,∠ACB=90°,
中,∠ACB=90°,![]() ,延长边BA至点D,使AD=AC,联结CD.
,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com