
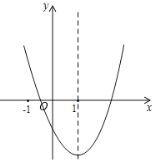
【题目】二次函数![]() 的图象如图所示,对称轴是直线
的图象如图所示,对称轴是直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数).其中结论正确的个数为( )
为实数).其中结论正确的个数为( )
A.1个B.2个C.3个D.4个
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,连接CO,过B作BD//OC交⊙O于D,连接AD交OC于G,延长AB、CD交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=4,DE=8,
①求CD的长;
②连接BC交AD于F,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
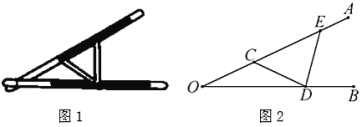
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图1所示的“三等分角仪”能三等分任一角.其抽象示意图如图2所示,由两根有槽的棒![]() ,
,![]() 组成,两根棒在
组成,两根棒在![]() 点相连并可绕
点相连并可绕![]() 转动.
转动.![]() 点固定,
点固定,![]() ,点
,点![]() ,
,![]() 可在槽中滑动,
可在槽中滑动,
(1)求证:![]() .
.
(2)若![]() ,
,
①求![]() 的度数;
的度数;
②求点![]() 到
到![]() 的距离.
的距离.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于G,过C点的切线与射线
于G,过C点的切线与射线![]() 相交于点E,直线
相交于点E,直线![]() 与
与![]() 交于点H,
交于点H,![]() ,
,![]() .
.

(Ⅰ)求![]() 的半径;
的半径;
(Ⅱ)将射线![]() 绕D点逆时针旋转,得射线
绕D点逆时针旋转,得射线![]() (如图2),
(如图2),![]() 与
与![]() 交于点M,与
交于点M,与![]() 及切线
及切线![]() 分别相交于点N,F,当
分别相交于点N,F,当![]() 时,求切线
时,求切线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“生物”学科学生的学习状况,某校从七年级学生中随机抽取了部分学生进行测试,测试结果分为四个等级:![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :及格,
:及格,![]() :不及格,并将结果绘制成了如下两幅不完整的统计图,请根据图中信息回答下列问题:
:不及格,并将结果绘制成了如下两幅不完整的统计图,请根据图中信息回答下列问题:
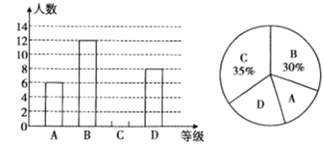
(1)共抽取了多少名学生进行测试?
(2)通过计算补全条形统计图;
(3)该校七年级学生共有450名学生,请你估计该校“生物”学科不及格的学生人数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
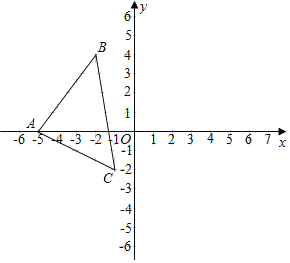
【题目】△ABC三顶点A(﹣5,0)、B(﹣2,4)、C(﹣1,﹣2),△A'B'C'与△ABC关于y轴对称.
(1)直接写出A'、B'、C'的坐标;
(2)画出△A'B'C';
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张正面分别写有数字:﹣3,﹣2,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不小于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为m的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为n的值,请用列表法或画树状图法,求点Q(m,n)在第四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com