
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图1所示的“三等分角仪”能三等分任一角.其抽象示意图如图2所示,由两根有槽的棒![]() ,
,![]() 组成,两根棒在
组成,两根棒在![]() 点相连并可绕
点相连并可绕![]() 转动.
转动.![]() 点固定,
点固定,![]() ,点
,点![]() ,
,![]() 可在槽中滑动,
可在槽中滑动,
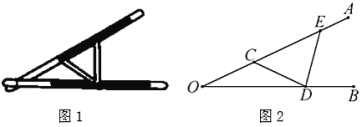
(1)求证:![]() .
.
(2)若![]() ,
,
①求![]() 的度数;
的度数;
②求点![]() 到
到![]() 的距离.
的距离.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E,F分别在AB,CD上,且![]() ,连接EF交BD于点O连接AO.若
,连接EF交BD于点O连接AO.若![]() ,,则
,,则![]() 的度数为( )
的度数为( )
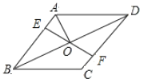
A.50°B.55°C.65°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,I是内心,AB=AC,O是AB边上一点,以点O为圆心,OB为半径的⊙O经过点I.
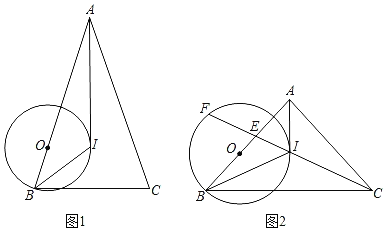
(1)求证:AI是⊙O的切线;
(2)如图2,连接CI交AB于点E,交⊙O于点F,若tan∠IBC=![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
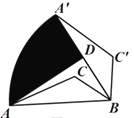
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,已知线段![]() ,现要在该网格内再确定格点
,现要在该网格内再确定格点![]() 和格点
和格点![]() ,某数学探究小组在探究时发现以下结论:以下结论不正确的是( )
,某数学探究小组在探究时发现以下结论:以下结论不正确的是( )

A.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为正方形的有2种;
为正方形的有2种;
B.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为菱形的(正方形除外)有3种;
为菱形的(正方形除外)有3种;
C.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为矩形的(正方形除外)有两种;
为矩形的(正方形除外)有两种;
D.不存在以![]() 为对角线的四边形
为对角线的四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第Ⅰ级:居民每户每月用水不超过18吨时,每吨收水费3元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过的部分每吨收水费4元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第Ⅰ、Ⅱ级标准收费,超过的部分每吨收水费6元.
现把上述水费阶梯收费办法称为方案①;假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费.
设一户居民月用水x吨.
(Ⅰ)根据题意填表:

(Ⅱ)设方案①应缴水费为![]() 元,方案②应缴水费为
元,方案②应缴水费为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)当![]() 时,通过计算说明居民选择哪种付费方式更合算.
时,通过计算说明居民选择哪种付费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系 ![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.
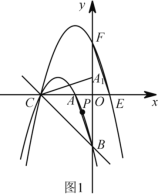
(1)求抛物线![]() 的解析式.
的解析式.
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若 ![]() ,求
,求![]() 点的坐标;
点的坐标;
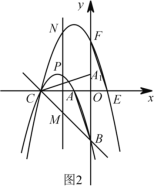
②如图![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
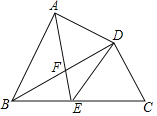
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则BF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com