
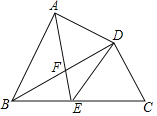
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则BF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
先利用含30度角的直角三角形的性质求出BD,再利用直角三角形的性质求出DE=BE=2,即:∠BDE=∠ABD,进而判断出DE∥AB,再求出AB=3,即可得出结论.
在Rt△BDC中,BC=4,∠DBC=30°,
∴BD=2![]() ,
,
∵∠BDC=90°,点E是BC中点,
∴DE=BE=CE=![]() BC=2,
BC=2,
∵∠DCB=30°,
∴∠BDE=∠DBC=30°,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠BDE,
∴DE∥AB,
∴△DEF∽△BAF,
∴![]() (相似三角形对应边成比例),
(相似三角形对应边成比例),
在Rt△ABD中,∠ABD=30°,BD=2![]() ,
,
∴AB=3,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴DF=![]() BD=
BD=![]() ×2
×2![]() =
=![]() ,
,
∴BF=![]() DF=
DF=![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图1所示的“三等分角仪”能三等分任一角.其抽象示意图如图2所示,由两根有槽的棒![]() ,
,![]() 组成,两根棒在
组成,两根棒在![]() 点相连并可绕
点相连并可绕![]() 转动.
转动.![]() 点固定,
点固定,![]() ,点
,点![]() ,
,![]() 可在槽中滑动,
可在槽中滑动,
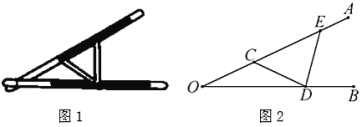
(1)求证:![]() .
.
(2)若![]() ,
,
①求![]() 的度数;
的度数;
②求点![]() 到
到![]() 的距离.
的距离.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
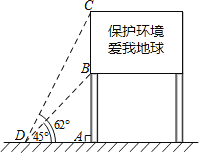
【题目】如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球”的宣传牌.已知立杆AB的高度是3m,从地面上某处D点测得宣传牌顶端C点和底端B点的仰角分别是62°和45°.求宣传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
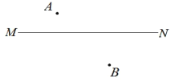
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点A的坐标为
中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,且
,且![]() ,
,![]() .给出如下定义:若平面上存在一点P,使
.给出如下定义:若平面上存在一点P,使![]() 是以线段
是以线段![]() 为斜边的直角三角形,则称点P为点A、点B的“直角点”.
为斜边的直角三角形,则称点P为点A、点B的“直角点”.
(1)已知点A的坐标为![]() .
.
①若点B的坐标为![]() ,在点
,在点![]() 、
、![]() 和
和![]() 中,是点A、点B的“直角点”的是_________;
中,是点A、点B的“直角点”的是_________;
②点B在x轴的正半轴上,且![]() ,当直线
,当直线![]() 上存在点A、点B的“直角点”时,求b的取值范围;
上存在点A、点B的“直角点”时,求b的取值范围;
(2)![]() 的半径为r,点
的半径为r,点![]() 为点
为点![]() 、点
、点![]() 的“直角点”,若使得
的“直角点”,若使得![]() 与
与![]() 有交点,直接写出半径r的取值范围.
有交点,直接写出半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张正面分别写有数字:﹣3,﹣2,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不小于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为m的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为n的值,请用列表法或画树状图法,求点Q(m,n)在第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=![]() ;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为1,其中正确的有( )
;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为1,其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
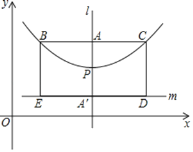
【题目】如图,在顶点为P的抛物线![]() 的对称轴l上取
的对称轴l上取![]() ,过A作
,过A作![]() 交抛物线于B,C两点(B在C左侧),点
交抛物线于B,C两点(B在C左侧),点![]() 和点A关于点P对称,过
和点A关于点P对称,过![]() 作
作![]() ,又分别过B,C作
,又分别过B,C作![]() ,垂足为E,D,在这里我们把点A叫抛物线的焦点,BC叫抛物线的直径,矩形BCDE叫抛物线的焦点矩形.
,垂足为E,D,在这里我们把点A叫抛物线的焦点,BC叫抛物线的直径,矩形BCDE叫抛物线的焦点矩形.
(1)直接写出抛物线![]() 的焦点坐标及其直径;
的焦点坐标及其直径;
(2)求抛物线![]() 的焦点坐标及其直径;
的焦点坐标及其直径;
(3)已知抛物线![]() 的直径为
的直径为![]() ,求a的值;
,求a的值;
(4)①已知抛物线![]() 的焦点矩形的面积为2,求a的值;
的焦点矩形的面积为2,求a的值;
②直接写出抛物线![]() 的焦点矩形与抛物线
的焦点矩形与抛物线![]() 有两个公共点时m的取值范围.
有两个公共点时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com