
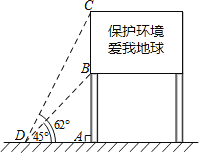
【题目】如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球”的宣传牌.已知立杆AB的高度是3m,从地面上某处D点测得宣传牌顶端C点和底端B点的仰角分别是62°和45°.求宣传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,I是内心,AB=AC,O是AB边上一点,以点O为圆心,OB为半径的⊙O经过点I.
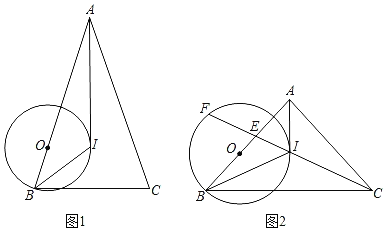
(1)求证:AI是⊙O的切线;
(2)如图2,连接CI交AB于点E,交⊙O于点F,若tan∠IBC=![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第Ⅰ级:居民每户每月用水不超过18吨时,每吨收水费3元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过的部分每吨收水费4元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第Ⅰ、Ⅱ级标准收费,超过的部分每吨收水费6元.
现把上述水费阶梯收费办法称为方案①;假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费.
设一户居民月用水x吨.
(Ⅰ)根据题意填表:

(Ⅱ)设方案①应缴水费为![]() 元,方案②应缴水费为
元,方案②应缴水费为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)当![]() 时,通过计算说明居民选择哪种付费方式更合算.
时,通过计算说明居民选择哪种付费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系 ![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.
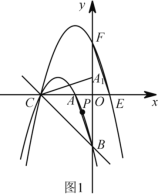
(1)求抛物线![]() 的解析式.
的解析式.
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若 ![]() ,求
,求![]() 点的坐标;
点的坐标;
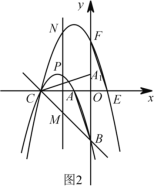
②如图![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价![]() (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD是由三个全等矩形拼成的,AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N,设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3.若S1+S3=30,则S2的值为( ).
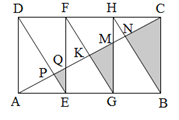
A.6B.8
C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,经过A、B、C三点的⊙O与AD相切于点A,经过点C的切线与AD的延长线相交于点P,连接AC.
(1)求证:AB=AC;
(2)若AB=4,⊙O的半径为![]() ,求PD的长.
,求PD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则BF的长为( )
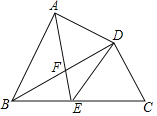
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.

(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连接EF,试判别四边形BCEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com