
【题目】如图1,在△ABC中,I是内心,AB=AC,O是AB边上一点,以点O为圆心,OB为半径的⊙O经过点I.
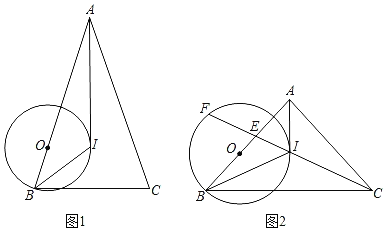
(1)求证:AI是⊙O的切线;
(2)如图2,连接CI交AB于点E,交⊙O于点F,若tan∠IBC=![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2)![]() =
=![]() .
.
【解析】
(1)延长AI交BC于D,连接OI.由I是△ABC的内心,得到BI平分∠ABC,AI平分∠BAC.求得∠1=∠3,推出OI∥BD,得到OI⊥AI.于是得到结论;
(2)连接BF,过B作BM⊥CF于M由(1)得AD垂直平分BC,求得BI=CI,根据等腰三角形的性质得到∠1=∠4,设法证得FB∥AD,证得△AEI~△BEF,得到![]() .设ID=a,求得
.设ID=a,求得![]() ,根据三角函数的定义即可得到结论.
,根据三角函数的定义即可得到结论.
(1)证明:延长AI交BC于D,连接OI.

∵I是△ABC的内心,
∴BI平分∠ABC,AI平分∠BAC.
∴∠1=∠3,
∵AB=AC,
∴AD⊥BC.
又∵OB=OI,
∴∠3=∠2.
∴∠1=∠2.
∴OI∥BD,
∴OI⊥AI,
∴AI为⊙O的切线;
(2)解:连接BF,过B作BM⊥CF于M,
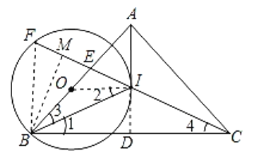
由(1)得AD垂直平分BC,
∴BI=CI,
∴∠1=∠4
故∠1=∠2=∠3=∠4=α,
∴∠BOI=180°﹣2α,
∴∠F=![]() ∠BOI=90°﹣α,
∠BOI=90°﹣α,
∴∠F+∠4=90°,
∴∠FBC=∠ADC=90°,
∴FB∥AD,
∴△BEF~△AEI,
∴![]() .
.
∵DI∥BF,BD=CD,
∴CI=FI,
∴BF=2ID,
故![]() ,
,
设ID=a,
∵![]() ,
,
∴![]() ,
,
由面积法:![]() ,
,
∴![]() ,
,
又∠MIB=2∠1=∠ABD,
∴tan∠MIB=tan∠ABD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ .
.


科目:初中数学 来源: 题型:
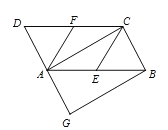
【题目】如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.
(1)求证:△ADF≌△CBE;
(2)若四边形AGBC是矩形,判断四边形AECF是什么特殊的四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新型冠状病毒疫情期间,某校学生主动发起为武汉加油捐款活动,为了了解学生捐款金额(单位:元),随机调查了该校的部分学生,根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
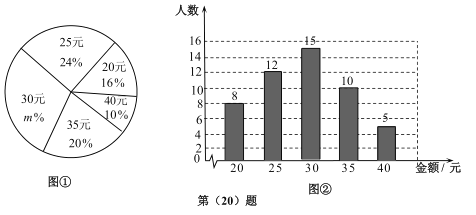
(Ⅰ)本次接受调查的学生人数为_________,图①中m的值为_________;
(Ⅱ)求统计的这组学生捐款数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组学生捐款数据的样本数据,若该校共有1800名学生,估计该校此次捐款总金额为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图1所示的“三等分角仪”能三等分任一角.其抽象示意图如图2所示,由两根有槽的棒![]() ,
,![]() 组成,两根棒在
组成,两根棒在![]() 点相连并可绕
点相连并可绕![]() 转动.
转动.![]() 点固定,
点固定,![]() ,点
,点![]() ,
,![]() 可在槽中滑动,
可在槽中滑动,
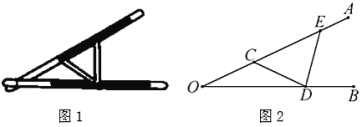
(1)求证:![]() .
.
(2)若![]() ,
,
①求![]() 的度数;
的度数;
②求点![]() 到
到![]() 的距离.
的距离.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球”的宣传牌.已知立杆AB的高度是3m,从地面上某处D点测得宣传牌顶端C点和底端B点的仰角分别是62°和45°.求宣传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
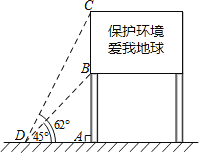
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com