
【题目】如图,扇形![]() ,且
,且![]() ,
,![]() ,
,![]() 为弧
为弧![]() 上任意一点,过
上任意一点,过![]() 点作
点作![]() 于点
于点![]() ,设
,设![]() 的内心为
的内心为![]() ,连接
,连接![]() 、
、![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,内心
时,内心![]() 所经过的路径长为________.
所经过的路径长为________.
【答案】![]() .
.
【解析】
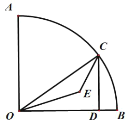
根据E为直角三角形OCD的内心,求出∠OEC=135°,连接BE,证明△OCE≌△OBE,得到∠OEB=135°,得到点E路径为以OB为弦,所对圆心角为135°的圆弧,构造⊙G,求出∠G=90°,![]() ,根据弧长公式计算即可.
,根据弧长公式计算即可.
解:如图,∵![]() ,
,
∴∠COD+∠OCD=90°,
∵E为直角三角形OCD的内心,
∴OE、CE分别平分∠COD、∠OCD,
∴∠OEC=![]() ,
,
连接BE,
∵OE=OE,OC=OC,∠COE=∠BOE
∴△COE≌△BOE
∴∠OEB=∠OEC=135°
∴点E的路径为以OB为弦,所对圆心角为135°的圆弧,
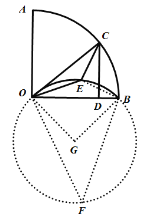
过点O、E、B作圆G,作圆内接四边形OEBF,则∠F=45°,
∴∠G=90°,
∵OG=OB,OB=4,
∴OG=![]() ,
,
∴弧OB长为:![]() .
.
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+15分别交x轴、y轴于点A,B,交直线y=
x+15分别交x轴、y轴于点A,B,交直线y=![]() x于点M.动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒.
x于点M.动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒.
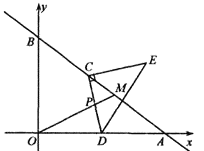
(1)求点A的坐标和AM的长.
(2)当t=5时,线段CD交OM于点P,且PC=PD,求a的值.
(3)在点C的整个运动过程中,
①直接用含t的代数式表示点C的坐标.
②利用(2)的结论,以C为直角顶点作等腰直角△CDE(点C,D,E按逆时针顺序排列),当OM与△CDE的一边平行时,求所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
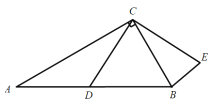
【题目】如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( )
A.![]() -1B.
-1B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E,F分别在AB,CD上,且![]() ,连接EF交BD于点O连接AO.若
,连接EF交BD于点O连接AO.若![]() ,,则
,,则![]() 的度数为( )
的度数为( )
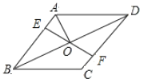
A.50°B.55°C.65°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
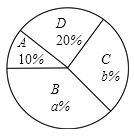
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛.并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级记为![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :一般,
:一般,![]() :较差),并制作了如下统计图表(部分信息未给出).
:较差),并制作了如下统计图表(部分信息未给出).
等级 | 人数 |
|
|
| 20 |
|
|
| 10 |
请根据统计图表中的信息解答下列问题:
(1)这次共抽取了______名参加演讲比赛的学生,统汁图中![]() ________,
________,![]() _______;
_______;
(2)求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数;
(3)若该校学生共2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的学生有多少人?
(4)若演讲比赛成绩为![]() 等级的学生中恰好有2名女生,其余的学生为男生,从
等级的学生中恰好有2名女生,其余的学生为男生,从![]() 等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
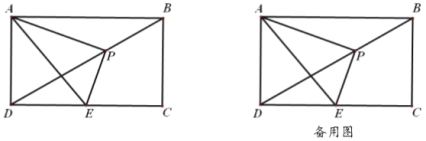
(1)求证:![]() ;
;
(2)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值;
的值;
(3)在点![]() 运动过程中,当
运动过程中,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,I是内心,AB=AC,O是AB边上一点,以点O为圆心,OB为半径的⊙O经过点I.
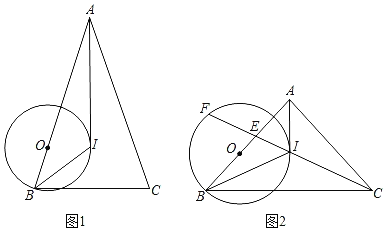
(1)求证:AI是⊙O的切线;
(2)如图2,连接CI交AB于点E,交⊙O于点F,若tan∠IBC=![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第Ⅰ级:居民每户每月用水不超过18吨时,每吨收水费3元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过的部分每吨收水费4元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第Ⅰ、Ⅱ级标准收费,超过的部分每吨收水费6元.
现把上述水费阶梯收费办法称为方案①;假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费.
设一户居民月用水x吨.
(Ⅰ)根据题意填表:

(Ⅱ)设方案①应缴水费为![]() 元,方案②应缴水费为
元,方案②应缴水费为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)当![]() 时,通过计算说明居民选择哪种付费方式更合算.
时,通过计算说明居民选择哪种付费方式更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com