
【题目】如图,在平面直角坐标系中,直线y=![]() x+15分别交x轴、y轴于点A,B,交直线y=
x+15分别交x轴、y轴于点A,B,交直线y=![]() x于点M.动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒.
x于点M.动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒.
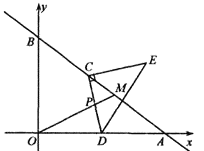
(1)求点A的坐标和AM的长.
(2)当t=5时,线段CD交OM于点P,且PC=PD,求a的值.
(3)在点C的整个运动过程中,
①直接用含t的代数式表示点C的坐标.
②利用(2)的结论,以C为直角顶点作等腰直角△CDE(点C,D,E按逆时针顺序排列),当OM与△CDE的一边平行时,求所有满足条件的t的值.
【答案】(1)A(20,0),10;(2)2;(3)①![]() ,②
,②![]() 或
或![]() 或4
或4
【解析】
(1)在![]() 中,令
中,令![]() ,得点A坐标,联立AB,OM解析式,求出点M坐标,过点M作
,得点A坐标,联立AB,OM解析式,求出点M坐标,过点M作![]() 轴垂线,垂足为G,由M坐标得出OG,MG,AG长度,由勾股定理可得结果.
轴垂线,垂足为G,由M坐标得出OG,MG,AG长度,由勾股定理可得结果.
(2)过点C作CQ![]()
![]() 轴交OM延长线与Q,证明△CPQ≌△DPO(AAS),得出CQ=OD,解出CQ长度即可.
轴交OM延长线与Q,证明△CPQ≌△DPO(AAS),得出CQ=OD,解出CQ长度即可.
(3)①作CK![]()
![]() 轴与K,由CK
轴与K,由CK![]()
![]() 轴,得
轴,得![]() ,解出
,解出![]() CK,代入
CK,代入![]() 中,得
中,得![]() .
.
②当OM![]() 于△CDE的一边,分三种情况进行讨论:当OM
于△CDE的一边,分三种情况进行讨论:当OM![]() CD 时,用
CD 时,用![]() 解得t值;当OM
解得t值;当OM![]() CE时,用CK=2DK解得t值;当OM
CE时,用CK=2DK解得t值;当OM![]() DE时,证明△CDK≌△CEG,用DH=2EH解得t值.
DE时,证明△CDK≌△CEG,用DH=2EH解得t值.
解:(1)当y=0时,![]() ,解得:x=20
,解得:x=20
∴点A(20,0);
∵两直线相交于点M
∴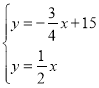 ,解得:
,解得:![]()
∴点M(12,6)
过点M作MG⊥OA于点G

∴OG=12,MG=6
∴AG=20-12=8
在Rt△AMG中,
![]() ;
;
(2)∵动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒![]() 个单位的速度从点0沿OA的方向运动,
个单位的速度从点0沿OA的方向运动,
∴当t=5时则AC=15,OD=5![]() ,AB=25
,AB=25
点C(8,9)
过点C作CQ∥x轴交OM的延长线于点Q,
∴点Q(18,9)
∴CQ=18-8=10,
∵CQ∥x轴
∴∠G=∠DOP
在△CPQ和△DPO中,

∴△CPQ≌△DPO(AAS)
∴CQ=OD
即5![]() =10,解之:
=10,解之:![]() =2.
=2.
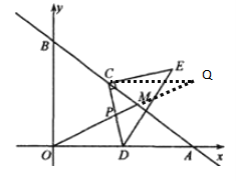
(3)解:①过点C作CK⊥x轴于点K,
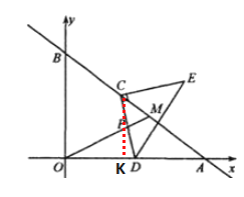
由题意可知AC=3t,AB=25,OB=15,
∴CK∥y轴,
∴△ACK∽△ABO
∴![]() 即
即![]()
解之:![]()
当![]() 时,则
时,则![]()
解之:![]()
∴点![]() ;
;
②由①可知CK=![]() , OK=
, OK=![]()
∵AC=3t,OD=2t,tan∠MOA=![]()
当CD∥OM时,

![]() 即
即![]()
解之:t=![]() ;
;
当CE∥OM时,

∴∠ECD=∠CPO=90°
∴∠DCK+∠CDK=∠DOP+∠CDK=90°
∴∠DCK=∠DOP
∴tan∠DCK=![]()
∴CK=2DK
∴DK=OD-OK=![]()
∴![]()
解之:![]() ;
;
当DE∥OM时,过点E作EH⊥x轴于点H,过点C作CK⊥x轴于点K,过点C作CG∥x轴交HE于点G,
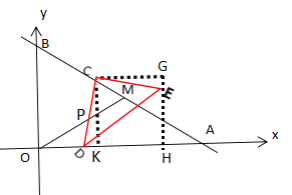
∵等腰直角△CDE
∴CD=CE
易证△CDK≌△CEG,
∴CK=CG=GH=![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
∵OM∥ED,
∴∠MOA=∠EDH,![]()
∴DH=2EH
∴![]()
解之:t=4.
∴t的值为![]() 或
或![]() 或4.
或4.


科目:初中数学 来源: 题型:
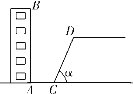
【题目】(2017黔东南州)如图,某校教学楼![]() 后方有一斜坡,已知斜坡
后方有一斜坡,已知斜坡![]() 的长为12米,视角
的长为12米,视角![]() 为60°,根据有关部门的规定,
为60°,根据有关部门的规定,![]() 时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡
时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡![]() 进行改造,在保持坡脚
进行改造,在保持坡脚![]() 不动的情况下,学校至少要把坡顶
不动的情况下,学校至少要把坡顶![]() 向后水平移动多少米才能保证教学楼的安全?(结果取整数,参考数据:
向后水平移动多少米才能保证教学楼的安全?(结果取整数,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,葫芦岛市九年级师生结束了两个多月的线上教学和学习,正式回归校园,在开学第一天,某校教导处老师为了解九年级学生对“新冠”传播与防治知识的掌握情况,随机抽取了部分学生进行了防疫知识的测试,测试后的成绩,按得分划分为
日,葫芦岛市九年级师生结束了两个多月的线上教学和学习,正式回归校园,在开学第一天,某校教导处老师为了解九年级学生对“新冠”传播与防治知识的掌握情况,随机抽取了部分学生进行了防疫知识的测试,测试后的成绩,按得分划分为![]() 四个等级,
四个等级,![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :及格,
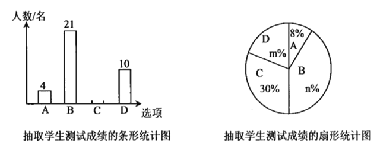
:及格,![]() :不及格,并绘制了如下不完整的条形统计图和扇形统计图.根据提供的信息,解答以下问题:
:不及格,并绘制了如下不完整的条形统计图和扇形统计图.根据提供的信息,解答以下问题:
(1)本次调查抽取的学生人数有多少人?
(2)扇形统计图中![]() ,
,![]() 并补全条形统计图;
并补全条形统计图;
(3)已知该校九年级有![]() 名学生,学校决定对“不及格”的学生进行一次防疫知识的培训,那么需要接受培训的学生大约有多少人?
名学生,学校决定对“不及格”的学生进行一次防疫知识的培训,那么需要接受培训的学生大约有多少人?
(4)已知“优秀”的同学有![]() 名男生和
名男生和![]() 名女生,从中随机抽取
名女生,从中随机抽取![]() 名进行防疫知识的交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
名进行防疫知识的交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如图所示的统计图:
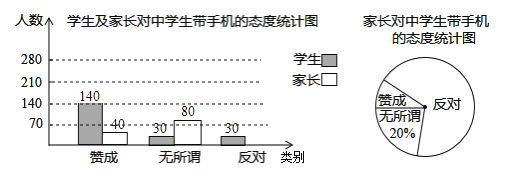
(1)求这次调查的家长人数,并补全图①:
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少?
(4)为更深入的了解学生的看法,又从“赞成”的学生甲、乙、丙、丁四人中随机选取2人,请用树状图法或列表法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
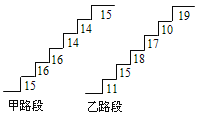
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差![]() ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差![]() :
:
(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
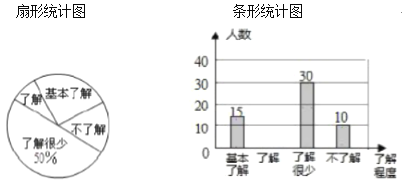
(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________![]() ;
;
(2)请补全条形统计图;
(3)若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为![]() ,现从中随机抽取
,现从中随机抽取![]() 人参加食品安全知识竞赛,则恰好抽到
人参加食品安全知识竞赛,则恰好抽到![]() 个男生和
个男生和![]() 个女生的概率________.
个女生的概率________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桌面上有四张正面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
(1)随机翻开一张卡片,正面所标数字大于![]() 的概率为 ;
的概率为 ;
(2)随机翻开一张卡片,从余下的三张卡片中再翻开一张,求翻开的两张卡片正面所标数字之和是偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com