
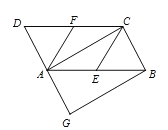
【题目】如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.
(1)求证:△ADF≌△CBE;
(2)若四边形AGBC是矩形,判断四边形AECF是什么特殊的四边形?并证明你的结论.
【答案】(1)证明见解析;(2)菱形,证明见解析.
【解析】
(1)由平行四边形的性质得出AD=BC,AD∥BC,∠D=∠ABC,AB=CD,然后通过E、F分别是边AB、CD的中点,得到DF=BE,由SAS证明△ADF≌△CBE即可;
(2)通过平行四边形ABCD可得四边形AECF为平行四边形,然后由矩形的性质得出∠ACB=90°,由直角三角形斜边上的中线性质得出CE=![]() AB=AE,即可证出四边形AECF为菱形.
AB=AE,即可证出四边形AECF为菱形.
(1)∵四边形ABCD是平行四边形,
∴AD=CB,∠D=∠ABC,AB=CD,
又∵E、F分别是边AB、CD的中点,
∴DF=BE,
在△ADF和△CBE中,
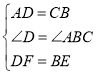
∴△ADF≌△CBE;
(2)四边形AECF为菱形;
证明:∵四边形ABCD是平行四边形,
∴CD∥AB,DC=AB,
又∵E、F分别是边AB、CD的中点,
∴CF=AE,
∴四边形AECF为平行四边形,
∵矩形AGBC,
∴∠ACB=90°,
又∵E为AB中点,
∴CE=![]() AB=AE,
AB=AE,
∴四边形AECF为菱形.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax-2amx+am2+2m-5与x轴交于A(x1,0),B(x2,0)(x1<x2)两点,顶点为P.
(1)当a=1,m=2时,求线段AB的长度;
(2)当a=2,若点P到x轴的距离与点P到y轴的距离相等,求该抛物线的解析式;
(3)若a= ![]() ,当2m-5≤x≤2m-2时,y的最大值为2,求m的值.
,当2m-5≤x≤2m-2时,y的最大值为2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
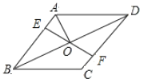
【题目】如图,在菱形ABCD中,点E,F分别在AB,CD上,且![]() ,连接EF交BD于点O连接AO.若
,连接EF交BD于点O连接AO.若![]() ,,则
,,则![]() 的度数为( )
的度数为( )
A.50°B.55°C.65°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
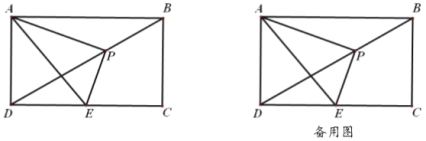
(1)求证:![]() ;
;
(2)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值;
的值;
(3)在点![]() 运动过程中,当
运动过程中,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,I是内心,AB=AC,O是AB边上一点,以点O为圆心,OB为半径的⊙O经过点I.
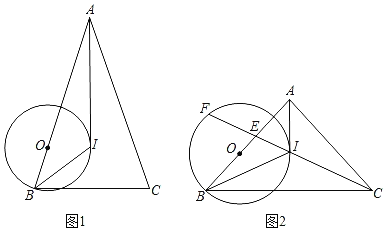
(1)求证:AI是⊙O的切线;
(2)如图2,连接CI交AB于点E,交⊙O于点F,若tan∠IBC=![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
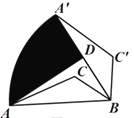
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系 ![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.
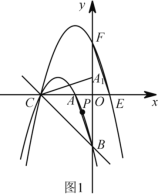
(1)求抛物线![]() 的解析式.
的解析式.
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若 ![]() ,求
,求![]() 点的坐标;
点的坐标;
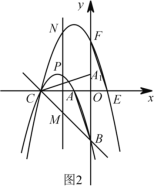
②如图![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com