
【题目】在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=![]() ;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为1,其中正确的有( )
;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为1,其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
根据正方形的性质、全等三角形的性质、勾股定理、三角形面积公式一一判断即可.
①∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠A=∠B=90°,
∵∠A=∠EDQ,∠AEP=∠QED,AE=ED,
∴△AEP≌△DEQ,故①正确,
②作PG⊥CD于G,EM⊥BC于M,
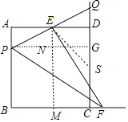
∴∠PGQ=∠EMF=90°,
∵EF⊥PQ,
∴∠PEF=90°,
∴∠PEN+∠NEF=90°,
∵∠NPE+∠NEP=90°,
∴∠NPE=∠NEF,
∵PG=EM,
∴△EFM≌△PQG,
∴EF=PQ,故②正确,
③连接QF.则QF=PF,PB2+BF2=QC2+CF2,设CF=x,则(2+x)2+12=32+x2,
∴x=1,故③错误,
④当P在A点时,Q与D重合,QC的中点H在DC的中点S处,
当P运动到B时,QC的中点H与D重合,
故EH扫过的面积为△ESD的面积的一半为![]() ,故④错误.
,故④错误.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第Ⅰ级:居民每户每月用水不超过18吨时,每吨收水费3元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过的部分每吨收水费4元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第Ⅰ、Ⅱ级标准收费,超过的部分每吨收水费6元.
现把上述水费阶梯收费办法称为方案①;假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费.
设一户居民月用水x吨.
(Ⅰ)根据题意填表:

(Ⅱ)设方案①应缴水费为![]() 元,方案②应缴水费为
元,方案②应缴水费为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)当![]() 时,通过计算说明居民选择哪种付费方式更合算.
时,通过计算说明居民选择哪种付费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,经过A、B、C三点的⊙O与AD相切于点A,经过点C的切线与AD的延长线相交于点P,连接AC.
(1)求证:AB=AC;
(2)若AB=4,⊙O的半径为![]() ,求PD的长.
,求PD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
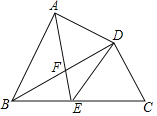
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则BF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.

(1)求证:直线DE是⊙O的切线;
(2)若⊙O半径为1,BC=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB =2∠EAB.
的中点,连接AE交BC于点F,∠ACB =2∠EAB.
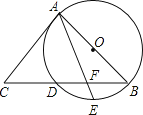
(1)求证:AC是⊙O的切线;
(2)若![]() ,
,![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
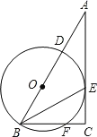
【题目】在 Rt△ABC 中,∠ACB=90°,BE 平分∠ABC,D 是边 AB 上一点,以 BD为直径的⊙O 经过点 E,且交 BC 于点 F.
(1)求证:AC 是⊙O 的切线;
(2)若 BC=8,⊙O 的半径为 5,求 CE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.

(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连接EF,试判别四边形BCEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
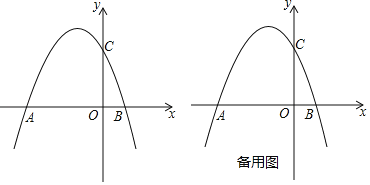
【题目】如图,抛物线y=﹣x2+bx+c交x轴于A、B两点,其中点A坐标为(﹣3,0),与y轴交于点C(0,3).
(1)求抛物线的函数解析式;
(2)点M为抛物线y=﹣x2+bx+c上异于点C的一个点,且S△OMC=![]() S△ABC,求点M的坐标;
S△ABC,求点M的坐标;
(3)若点P为x轴上方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AP、BP分别交抛物线的对称轴于点E、F.请问DE+DF是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com