
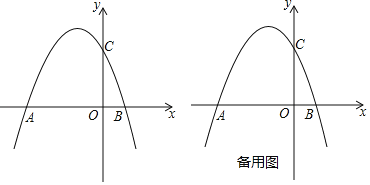
【题目】如图,抛物线y=﹣x2+bx+c交x轴于A、B两点,其中点A坐标为(﹣3,0),与y轴交于点C(0,3).
(1)求抛物线的函数解析式;
(2)点M为抛物线y=﹣x2+bx+c上异于点C的一个点,且S△OMC=![]() S△ABC,求点M的坐标;
S△ABC,求点M的坐标;
(3)若点P为x轴上方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AP、BP分别交抛物线的对称轴于点E、F.请问DE+DF是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)y=﹣x2﹣2x+3;(2)(2,﹣5)或(﹣2,3);(3)是定值,8
【解析】
(1)将点A、C的坐标代入抛物线表达式,即可求解;
(2)![]() S△ABC=
S△ABC=![]() ×
×![]() ×AB×OC=
×AB×OC=![]() ×4×3=3,而S△OMC=
×4×3=3,而S△OMC=![]() ×OC×|
×OC×|![]() |=
|=![]() |
|![]() |=3,即可求解;
|=3,即可求解;
(3)求出直线AP、BP的函数表达式,即可求解.
解:(1)将点A、C的坐标代入抛物线表达式得![]() ,解得
,解得![]() ,
,
故抛物线的表达式为:y=﹣x2﹣2x+3;
(2)对于抛物线y=﹣x2﹣2x+3,令y=0,则x=﹣3或1,
故点B(1,0),
∴![]() S△ABC=
S△ABC=![]() ×
×![]() ×AB×OC=
×AB×OC=![]() ×4×3=3,
×4×3=3,
∵S△OMC=![]() ×OC×|
×OC×|![]() |=
|=![]() |
|![]() |=3,解得:
|=3,解得:![]() =±2,
=±2,
故点M的坐标为(2,﹣5)或(﹣2,3);
(3)是定值,理由:
设点P的坐标为(m,﹣m2﹣2m+3),

设直线AP的表达式为:y=kx+t,则![]() ,解得
,解得![]() ,
,
故直线AP的表达式为:y=﹣(m﹣1)(x+3),
当x=![]() =﹣1时,y=2﹣2m,即点E(﹣1,2﹣2m),即DE=2﹣2m,
=﹣1时,y=2﹣2m,即点E(﹣1,2﹣2m),即DE=2﹣2m,
同理可得,直线BP的表达式为:y=﹣(m+3)(x﹣1),
当x=﹣1时,y=2m+6,故点F(﹣1,2m+6),即DF=2m+6,
∴DE+DF=2﹣2m+2m+6=8,为定值.


科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=![]() ;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为1,其中正确的有( )
;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为1,其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
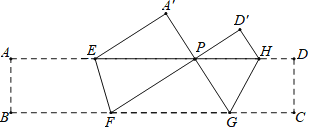
【题目】如图,已知点E,H在矩形ABCD的AD边上,点F,G在BC边上,将矩形ABCD沿EF,GH折叠,使点B和点C落在AD边上同一点P处.折叠后,点A的对应点为点A',点D的对应点为点D',若∠FPG=90°,A'E=3,D'H=1,则矩形ABCD的周长等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
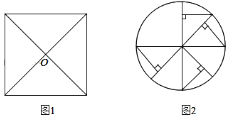
【题目】规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形 B.正五边形 C.菱形 D.正六边形
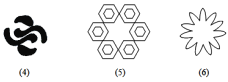
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);

(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;
A.0 B.1 C.2 D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
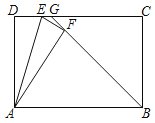
【题目】如图,矩形ABCD中,AB=6,AD=2![]() ,E是边CD上一点,将△ADE沿直线AE折叠得到△AFE,BF的延长线交边CD于点G,则DG的最大值为_____.
,E是边CD上一点,将△ADE沿直线AE折叠得到△AFE,BF的延长线交边CD于点G,则DG的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 内任意一点P,过P点作
内任意一点P,过P点作![]() 轴于点M,
轴于点M,![]() 轴于点N,连接
轴于点N,连接![]() ,则称
,则称![]() 的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
(1)点![]() 的垂点距离分别为________,___________,____________;
的垂点距离分别为________,___________,____________;
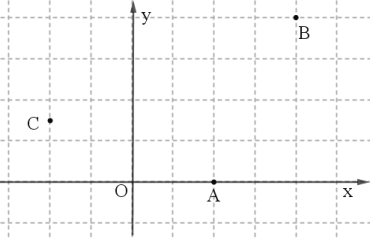
(2)点P在以![]() 为圆心,半径为3的
为圆心,半径为3的![]() 上运动,求出点P的垂点距离h的取值范围;
上运动,求出点P的垂点距离h的取值范围;
(3)点T为直线![]() 位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社会团体准备购进甲、乙两种防护服捐给一线抗疫人员,经了解,购进5件甲种防护服和4件乙种防护服需要2万元,购进10件甲种防护服和3件乙种防护服需要3万元.
(1)甲种防护服和乙种防护服每件各多少元?
(2)实际购买时,发现厂家有两种优惠方案,方案一:购买甲种防护服超过20件时,超过的部分按原价的8折付款,乙种防护服没有优惠;方案二:两种防护服都按原价的9折付款,该社会团体决定购买![]()
![]() 件甲种防护服和30件乙种防护服.
件甲种防护服和30件乙种防护服.
①求两种方案的费用![]() 与件数
与件数![]() 的函数解析式;
的函数解析式;
②请你帮该社会团体决定选择哪种方案更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com