
【题目】对于平面直角坐标系![]() 内任意一点P,过P点作
内任意一点P,过P点作![]() 轴于点M,
轴于点M,![]() 轴于点N,连接
轴于点N,连接![]() ,则称
,则称![]() 的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
(1)点![]() 的垂点距离分别为________,___________,____________;
的垂点距离分别为________,___________,____________;
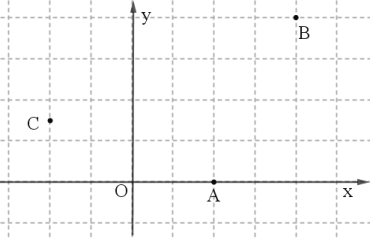
(2)点P在以![]() 为圆心,半径为3的
为圆心,半径为3的![]() 上运动,求出点P的垂点距离h的取值范围;
上运动,求出点P的垂点距离h的取值范围;
(3)点T为直线![]() 位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
【答案】(1)![]() ;(2)1≤
;(2)1≤![]() ≤ 5;(3)
≤ 5;(3)![]() 或
或![]()
【解析】
(1)运用勾股定理计算出三点的垂点距离;
(2)过点P作![]() 轴于点M,
轴于点M,![]() 轴于点N,易证四边形
轴于点N,易证四边形![]() 是矩形,所以OP=MN,则求点P的垂点距离h的取值范围,及求圆上一点P到坐标圆点O的取值范围;
是矩形,所以OP=MN,则求点P的垂点距离h的取值范围,及求圆上一点P到坐标圆点O的取值范围;
(3)设直线l与x轴,y轴的交点分别为![]() ,过点O作
,过点O作![]() 直线l于点M,以
直线l于点M,以![]() 为半径作
为半径作![]() ,交直线l于点N,过点
,交直线l于点N,过点![]() 分别作x轴的垂线,垂足分别为
分别作x轴的垂线,垂足分别为![]() ,求出OC,OD的距里,从而找到t的取值范围.
,求出OC,OD的距里,从而找到t的取值范围.
解:(1)如图所示:
∴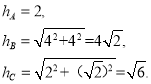 .
.

(2)如图,过点P作![]() 轴于点M,
轴于点M,![]() 轴于点N.
轴于点N.

![]() ,
,
![]() 四边形
四边形![]() 是矩形.
是矩形.
![]() .
.
![]() 点坐标为
点坐标为![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
(3)如图,设直线l与x轴,y轴的交点分别为![]() ,过点O作
,过点O作![]() 直线l于点M,以
直线l于点M,以![]() 为半径作
为半径作![]() ,交直线l于点N.
,交直线l于点N.

![]() ,
,
![]() .
.
过点![]() 分别作x轴的垂线,垂足分别为
分别作x轴的垂线,垂足分别为![]() ,
,
则![]() ,即
,即![]() .
.
![]() 是等边三角形,
是等边三角形,
![]() .
.
![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.

(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连接EF,试判别四边形BCEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于A、B两点,其中点A坐标为(﹣3,0),与y轴交于点C(0,3).
(1)求抛物线的函数解析式;
(2)点M为抛物线y=﹣x2+bx+c上异于点C的一个点,且S△OMC=![]() S△ABC,求点M的坐标;
S△ABC,求点M的坐标;
(3)若点P为x轴上方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AP、BP分别交抛物线的对称轴于点E、F.请问DE+DF是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
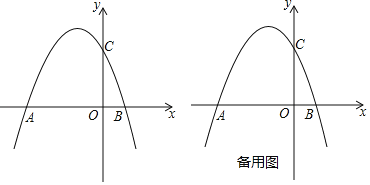
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师和学生一起去测量学校升旗台上旗杆AB的高度.如图,老师测得升旗台前斜坡AC的坡度为1:10(即AE:CE=1:10),学生小明站在离升旗台水平距离为35m(即CE=35m)处的C点,测得旗杆顶端B的仰角α=30°,已知小明身高CD=1.6m,求旗杆AB的高度.(参考数据:tan30°≈0.58,结果保留整数)
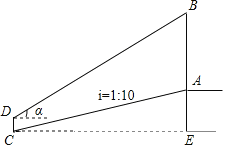
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() ,过点P作平行于x轴的直线,交直线
,过点P作平行于x轴的直线,交直线![]() 于点C,过点P作平行于y轴的直线交反比例函数
于点C,过点P作平行于y轴的直线交反比例函数![]() 的图象于点D,当
的图象于点D,当![]() 时,结合函数的图象,求出n的值.
时,结合函数的图象,求出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是指一个国家(或地区)在一定时期内生产活动的最终成果,常被公认为是衡量经济状况的最佳指标.截止2020年4月27日,对除西藏外的30个省区市第一季度有关
是指一个国家(或地区)在一定时期内生产活动的最终成果,常被公认为是衡量经济状况的最佳指标.截止2020年4月27日,对除西藏外的30个省区市第一季度有关![]() 的数据进行收集、整理、描述和分析.下面给出了部分信息:
的数据进行收集、整理、描述和分析.下面给出了部分信息:
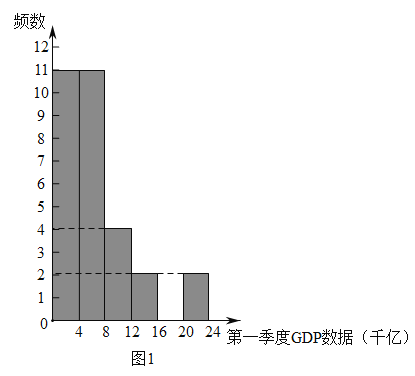
a.各省区市![]() 数据的频数分布直方图,如图1(数据分成6组,各组是
数据的频数分布直方图,如图1(数据分成6组,各组是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
b.2020年第一季度![]() 数据在这一组的是:4.6 4.9 5.0 5.1 5.3 5.4 6.3 7.4 7.5 7.8 7.8
数据在这一组的是:4.6 4.9 5.0 5.1 5.3 5.4 6.3 7.4 7.5 7.8 7.8
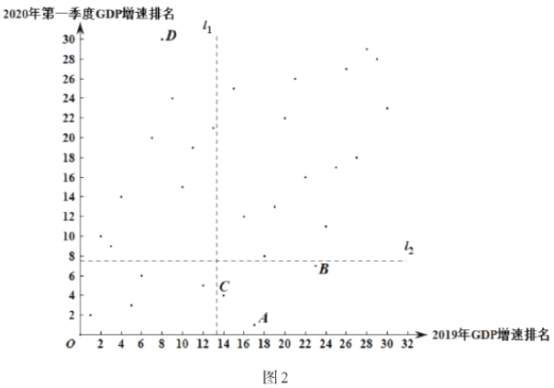
c.30个省区市2020年第一季度及2019年![]() 增速排名统计图,如图2:
增速排名统计图,如图2:
d.北京2020年第一季度![]() 数据约为7.5千亿,
数据约为7.5千亿,![]() 增速排名为第22.
增速排名为第22.
根据以上信息,回答下列问题:
(1)在30个省区市中,北京2020年第一季度![]() 的数据排名第______.
的数据排名第______.
(2)在30个省区市2020年第一季度及2019年![]() 增速排名统计图中,请在图中用“○”圈出代表北京的点.
增速排名统计图中,请在图中用“○”圈出代表北京的点.
(3)2020年第一季度![]() 增速排名位于北京之后的几个省份中,2019年
增速排名位于北京之后的几个省份中,2019年![]() 增速排名的最好成绩是第_______.
增速排名的最好成绩是第_______.
(4)下列推断合理的是___________.
①与2019年![]() 增速排名相比,在疫情冲击下,2020年全国第一季度增速排名,部分省市有较大下滑,如D代表的湖北排名下滑最多.
增速排名相比,在疫情冲击下,2020年全国第一季度增速排名,部分省市有较大下滑,如D代表的湖北排名下滑最多.
②A、B、C分别代表的新疆、广西、青海位于西部地区,多为人口净流出或少量净流入,经济发展主要依靠本地劳动力供给,疫后复工复产效率相对较高,相对于2019年![]() 增速排名位置靠前.
增速排名位置靠前.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小志自主创业,在网上经营一家水果店,销售的水果中有盒装草莓、荔枝、山竹,价格依次为40元/盒、60元/盒、80元/盒.为增加销量,小志对这三种水果进行促销:一次性购买水果的总价超过100元时,超过的部分打5折,每笔订单限购3盒.顾客支付成功后,小志会得到支付款的80%作为货款.
(1)顾客一笔订单购买了上述三种水果各一盒,则小志收到的货款是________元;
(2)小志在两笔订单中共售出原价180元的水果,则他收到的货款最少是________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC,BC交于点E,F. 过点F作⊙O的切线交AB于点M.
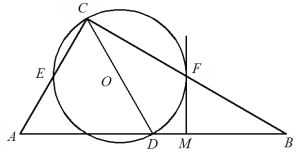
(1)求证:MF⊥AB;
(2)若⊙O的直径是6,填空:
①连接OF,OM,当FM= 时,四边形OMBF是平行四边形;
②连接DE,DF,当AC= 时,四边形CEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状肺炎给人类带来了灾难.口罩是抗击新冠肺炎的重要战略物资,国家在必要时进行价格限制,以保持价格稳定.某公司生产的口罩售价与天数的函数关系如图所示(曲线部分是以![]() 轴为对称轴的抛物线一部分).
轴为对称轴的抛物线一部分).
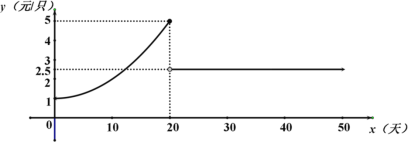
(1)求口罩销售价格![]() (元)与天数
(元)与天数![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)若这种口罩每只成本![]() (元)与天数
(元)与天数![]() 之间的关系为:
之间的关系为: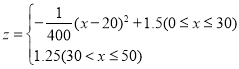 .那么这种口罩在第几天售出后单只利润最大?最大利润为多少?
.那么这种口罩在第几天售出后单只利润最大?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com