
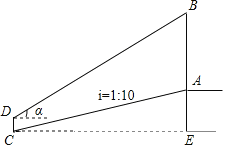
【题目】数学活动课上,老师和学生一起去测量学校升旗台上旗杆AB的高度.如图,老师测得升旗台前斜坡AC的坡度为1:10(即AE:CE=1:10),学生小明站在离升旗台水平距离为35m(即CE=35m)处的C点,测得旗杆顶端B的仰角α=30°,已知小明身高CD=1.6m,求旗杆AB的高度.(参考数据:tan30°≈0.58,结果保留整数)
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
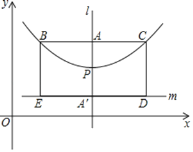
【题目】如图,在顶点为P的抛物线![]() 的对称轴l上取
的对称轴l上取![]() ,过A作
,过A作![]() 交抛物线于B,C两点(B在C左侧),点
交抛物线于B,C两点(B在C左侧),点![]() 和点A关于点P对称,过
和点A关于点P对称,过![]() 作
作![]() ,又分别过B,C作
,又分别过B,C作![]() ,垂足为E,D,在这里我们把点A叫抛物线的焦点,BC叫抛物线的直径,矩形BCDE叫抛物线的焦点矩形.
,垂足为E,D,在这里我们把点A叫抛物线的焦点,BC叫抛物线的直径,矩形BCDE叫抛物线的焦点矩形.
(1)直接写出抛物线![]() 的焦点坐标及其直径;
的焦点坐标及其直径;
(2)求抛物线![]() 的焦点坐标及其直径;
的焦点坐标及其直径;
(3)已知抛物线![]() 的直径为
的直径为![]() ,求a的值;
,求a的值;
(4)①已知抛物线![]() 的焦点矩形的面积为2,求a的值;
的焦点矩形的面积为2,求a的值;
②直接写出抛物线![]() 的焦点矩形与抛物线
的焦点矩形与抛物线![]() 有两个公共点时m的取值范围.
有两个公共点时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
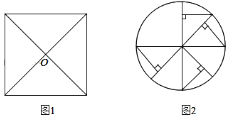
【题目】规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形 B.正五边形 C.菱形 D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);

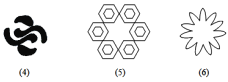
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;
A.0 B.1 C.2 D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
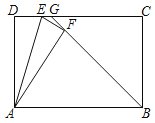
【题目】如图,矩形ABCD中,AB=6,AD=2![]() ,E是边CD上一点,将△ADE沿直线AE折叠得到△AFE,BF的延长线交边CD于点G,则DG的最大值为_____.
,E是边CD上一点,将△ADE沿直线AE折叠得到△AFE,BF的延长线交边CD于点G,则DG的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如下表:
餐食种类 | 价格(单位:元) |
汉堡套餐 | 40 |
鸡翅 | 16 |
鸡块 | 15 |
冰激凌 | 14 |
蔬菜沙拉 | 9 |
促销活动:
(1)汉堡套餐5折优惠,每单仅限一套;
(2)全部商品(包括打折套餐)满20元减4元,满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花____________元(含送餐费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 内任意一点P,过P点作
内任意一点P,过P点作![]() 轴于点M,
轴于点M,![]() 轴于点N,连接
轴于点N,连接![]() ,则称
,则称![]() 的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
(1)点![]() 的垂点距离分别为________,___________,____________;
的垂点距离分别为________,___________,____________;
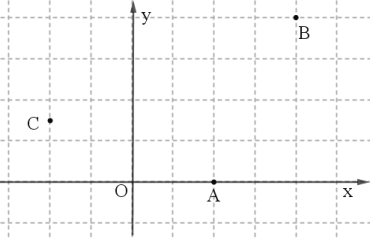
(2)点P在以![]() 为圆心,半径为3的
为圆心,半径为3的![]() 上运动,求出点P的垂点距离h的取值范围;
上运动,求出点P的垂点距离h的取值范围;
(3)点T为直线![]() 位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转45°,得到
顺时针旋转45°,得到![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
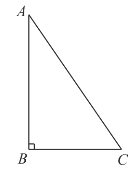
(1)根据题意补全图形;
(2)判断![]() 的形状,并证明;
的形状,并证明;
(3)连接![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
温馨提示:在解决第(3)问的过程中,如果你遇到困难,可以参考下面几种解法的主要思路.
解法1的主要思路:
延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,可证
,可证![]() ,再证
,再证![]() 是等腰直角三角形.
是等腰直角三角形.
解法2的主要思路:
过点![]() 作
作![]() 于点
于点![]() ,可证
,可证![]() 是等腰直角三角形,再证
是等腰直角三角形,再证![]() .
.
解法3的主要思路:
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,用含
,用含![]() 或
或![]() 的式子表示
的式子表示![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,将点
,将点![]() 向右平移2个单位得到点
向右平移2个单位得到点![]() .
.
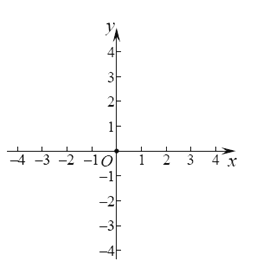
(1)求点![]() 坐标;
坐标;
(2)如果一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,且点
,且点![]() 的横坐标为1.
的横坐标为1.
①![]() 时,求
时,求![]() 的值;
的值;
②当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com