
【题目】小志自主创业,在网上经营一家水果店,销售的水果中有盒装草莓、荔枝、山竹,价格依次为40元/盒、60元/盒、80元/盒.为增加销量,小志对这三种水果进行促销:一次性购买水果的总价超过100元时,超过的部分打5折,每笔订单限购3盒.顾客支付成功后,小志会得到支付款的80%作为货款.
(1)顾客一笔订单购买了上述三种水果各一盒,则小志收到的货款是________元;
(2)小志在两笔订单中共售出原价180元的水果,则他收到的货款最少是________元.
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
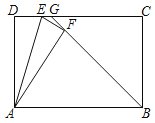
【题目】如图,矩形ABCD中,AB=6,AD=2![]() ,E是边CD上一点,将△ADE沿直线AE折叠得到△AFE,BF的延长线交边CD于点G,则DG的最大值为_____.
,E是边CD上一点,将△ADE沿直线AE折叠得到△AFE,BF的延长线交边CD于点G,则DG的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 内任意一点P,过P点作
内任意一点P,过P点作![]() 轴于点M,
轴于点M,![]() 轴于点N,连接
轴于点N,连接![]() ,则称
,则称![]() 的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
的长度为点P的垂点距离,记为h.特别地,点P与原点重合时,垂点距离为0.
(1)点![]() 的垂点距离分别为________,___________,____________;
的垂点距离分别为________,___________,____________;
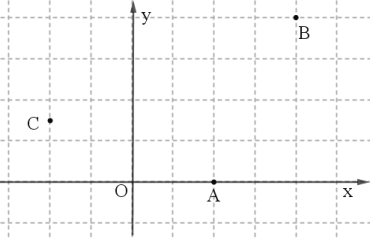
(2)点P在以![]() 为圆心,半径为3的
为圆心,半径为3的![]() 上运动,求出点P的垂点距离h的取值范围;
上运动,求出点P的垂点距离h的取值范围;
(3)点T为直线![]() 位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
位于第二象限内的一点,对于点T的垂点距离h的每个值有且仅有一个点T与之对应,求点T的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() 与x轴交于点
与x轴交于点![]() ,且
,且![]() .抛物线与y轴交于点C,将点C向上移动1个单位得到点D.
.抛物线与y轴交于点C,将点C向上移动1个单位得到点D.
(1)求抛物线对称轴;
(2)求点D纵坐标(用含有a的代数式表示);
(3)已知点![]() ,若抛物线与线段
,若抛物线与线段![]() 只有一个公共点,求a的取值范围.
只有一个公共点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转45°,得到
顺时针旋转45°,得到![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)根据题意补全图形;
(2)判断![]() 的形状,并证明;
的形状,并证明;
(3)连接![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
温馨提示:在解决第(3)问的过程中,如果你遇到困难,可以参考下面几种解法的主要思路.
解法1的主要思路:
延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,可证
,可证![]() ,再证
,再证![]() 是等腰直角三角形.
是等腰直角三角形.
解法2的主要思路:
过点![]() 作
作![]() 于点
于点![]() ,可证
,可证![]() 是等腰直角三角形,再证
是等腰直角三角形,再证![]() .
.
解法3的主要思路:
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,用含
,用含![]() 或
或![]() 的式子表示
的式子表示![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
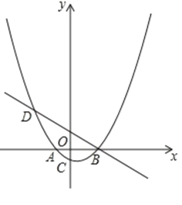
【题目】如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣![]() x+
x+![]() 抛物线的另一交点为D,且点D的横坐标为﹣5.
抛物线的另一交点为D,且点D的横坐标为﹣5.
(1)求抛物线的函数表达式;
(2)该二次函数图象上有一点P(x,y)使得S△BCD=S△ABP,求点P的坐标;
(3)设F为线段BD上一点(不含端点),连接AF,求2AF+DF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社会团体准备购进甲、乙两种防护服捐给一线抗疫人员,经了解,购进5件甲种防护服和4件乙种防护服需要2万元,购进10件甲种防护服和3件乙种防护服需要3万元.
(1)甲种防护服和乙种防护服每件各多少元?
(2)实际购买时,发现厂家有两种优惠方案,方案一:购买甲种防护服超过20件时,超过的部分按原价的8折付款,乙种防护服没有优惠;方案二:两种防护服都按原价的9折付款,该社会团体决定购买![]()
![]() 件甲种防护服和30件乙种防护服.
件甲种防护服和30件乙种防护服.
①求两种方案的费用![]() 与件数
与件数![]() 的函数解析式;
的函数解析式;
②请你帮该社会团体决定选择哪种方案更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
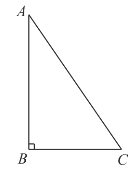
【题目】已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com