
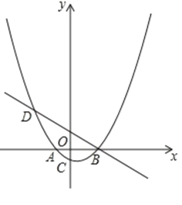
【题目】如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣![]() x+
x+![]() 抛物线的另一交点为D,且点D的横坐标为﹣5.
抛物线的另一交点为D,且点D的横坐标为﹣5.
(1)求抛物线的函数表达式;
(2)该二次函数图象上有一点P(x,y)使得S△BCD=S△ABP,求点P的坐标;
(3)设F为线段BD上一点(不含端点),连接AF,求2AF+DF的最小值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ;(2)(
;(2)(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)
);(3)![]()
【解析】
(1)求出点D的坐标,利用待定系数法求出a的值即可.
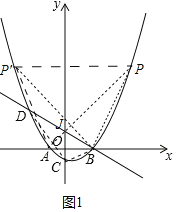
(2)如图1中,设直线BD交y轴于J,则J(0,![]() ).连接CD,BC.由S△PAB=10
).连接CD,BC.由S△PAB=10![]() ,推出
,推出![]() ×6×|yP|=10,推出yP=
×6×|yP|=10,推出yP=![]() ,再利用待定系数法构建方程求出点P的坐标即可.
,再利用待定系数法构建方程求出点P的坐标即可.
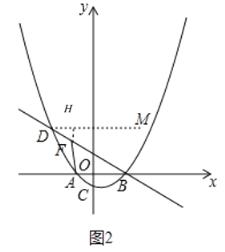
(3)如图2中,过点D作DM平行于x轴,首先证明∠BDM=∠DBA=30°,过F作FJ⊥DM于J,则有sin30°=![]() ,推出HF=
,推出HF=![]() ,推出2AF+DF=2(AF+
,推出2AF+DF=2(AF+![]() )=2(AF+HF),当A、F、H三点共线时,即AH⊥DM时,2AF+DF=2(AF+HF)取最小值.
)=2(AF+HF),当A、F、H三点共线时,即AH⊥DM时,2AF+DF=2(AF+HF)取最小值.
解:(1)抛物线y=a(x+2)(x﹣4),令y=0,解得x=﹣2或x=4,
∴A(﹣2,0),B(4,0).
∵直线y=![]() ,
,
当x=﹣5时,y=![]()
∴D(﹣5,![]() ),
),
∵点D(﹣5,3)在抛物线y=a(x+2)(x﹣4)上,
∴a(﹣5+2)(﹣5﹣4)=![]() ,
,
∴a=![]() .
.
∴抛物线的函数表达式为:y=![]() .
.
(2)如图1中,设直线BD交y轴于J,则J(0,![]() ).连接CD,BC.
).连接CD,BC.
∵S△BDC=![]()
∴S△PAB=![]() ,
,
∴![]() ×6×|yP|=
×6×|yP|=![]()
yP=![]() ,
,
当y=![]() 时,
时, ![]() ,
,
解得x=![]() ,
,
∴P![]() 或
或![]() ,
,
当![]()
方程无解,
∴满足条件的点P的坐标为![]() 或
或![]() .
.
(3)如图2中,过点D作DM平行于x轴,作FH⊥DM于H,
∵D![]() ,B(4,0),
,B(4,0),
∴tan∠DBA=![]() ,
,
∴∠DBA=30°
∴∠BDM=∠DBA=30°,过F作FJ⊥DM于J,
则有sin30°=![]() ,
,
∴![]() ,
,
∴2AF+DF=2(AF+![]() )=2(AF+HF),当A、F、H三点共线时,
)=2(AF+HF),当A、F、H三点共线时,
即AH⊥DM时,2AF+DF=2(AF+HF)取最小值![]() .
.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
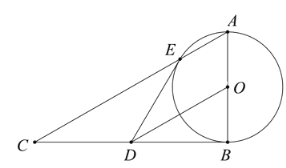
【题目】如图,直角三角形ABC中,∠ABC=90°,以边AB为直径作圆O,交AC于点E,点D是BC的中点,连接DE
(1)判断DE与圆O的关系,说明理由;
(2)若AB=4,DE=![]() ,点G是圆上出E、B外的任意一点,则∠EGB=______°(直接写出答案).
,点G是圆上出E、B外的任意一点,则∠EGB=______°(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() ,过点P作平行于x轴的直线,交直线
,过点P作平行于x轴的直线,交直线![]() 于点C,过点P作平行于y轴的直线交反比例函数
于点C,过点P作平行于y轴的直线交反比例函数![]() 的图象于点D,当
的图象于点D,当![]() 时,结合函数的图象,求出n的值.
时,结合函数的图象,求出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小志自主创业,在网上经营一家水果店,销售的水果中有盒装草莓、荔枝、山竹,价格依次为40元/盒、60元/盒、80元/盒.为增加销量,小志对这三种水果进行促销:一次性购买水果的总价超过100元时,超过的部分打5折,每笔订单限购3盒.顾客支付成功后,小志会得到支付款的80%作为货款.
(1)顾客一笔订单购买了上述三种水果各一盒,则小志收到的货款是________元;
(2)小志在两笔订单中共售出原价180元的水果,则他收到的货款最少是________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,则∠CMA的度数为( )
EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,则∠CMA的度数为( )
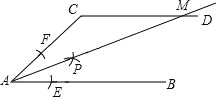
A.30°B.35°C.70°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC,BC交于点E,F. 过点F作⊙O的切线交AB于点M.
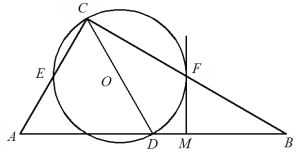
(1)求证:MF⊥AB;
(2)若⊙O的直径是6,填空:
①连接OF,OM,当FM= 时,四边形OMBF是平行四边形;
②连接DE,DF,当AC= 时,四边形CEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欧几里得在《几何原本》中,记载了用图解法解方程![]() 的方法,类似地我们可以用折纸的方法求方程
的方法,类似地我们可以用折纸的方法求方程![]() 的一个正根.如图,一张边长为1的正方形的纸片
的一个正根.如图,一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,再折出线段
,再折出线段![]() ,然后通过沿线段
,然后通过沿线段![]() 折叠使
折叠使![]() 落在线段
落在线段![]() 上,得到点
上,得到点![]() 的新位置
的新位置![]() ,并连接
,并连接![]() 、
、![]() ,此时,在下列四个选项中,有一条线段的长度恰好是方程
,此时,在下列四个选项中,有一条线段的长度恰好是方程![]() 的一个正根,则这条线段是( )
的一个正根,则这条线段是( )
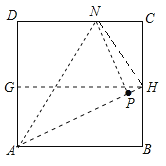
A.线段![]() B.线段
B.线段![]() C.线段
C.线段![]() D.线段
D.线段![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了![]() 条各具特色的趣玩路线,分别是:
条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家, 爱园艺”、
.“爱我家, 爱园艺”、![]() .“园艺小清新之旅”、
.“园艺小清新之旅”、![]() .“快速车览之旅”.李明和张春各自在这
.“快速车览之旅”.李明和张春各自在这![]() 条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李明选择线路![]() .“ 爱我家,爱园艺”的概率为 ;
.“ 爱我家,爱园艺”的概率为 ;
(2)用画树状图或列表的方法,求李明和张春恰好选择同一线路游览的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1和2,四边形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() .
.
(1)①如图 1,若![]() 、
、![]() 都是直角,把
都是直角,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,使
,使![]() 与
与![]() 重合,则能证得
重合,则能证得![]() ,请写出推理过程;
,请写出推理过程;
②如图 2,若![]() 、
、![]() 都不是直角,则当
都不是直角,则当![]() 与
与![]() 满足数量关系_______时,仍有
满足数量关系_______时,仍有![]() ;
;
(2)拓展:如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 均在边
均在边![]() 上,且
上,且![]() .若
.若![]() ,求
,求![]() 的长.
的长.
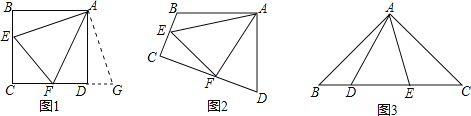
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com