
分析 (1)求的是工效,工作总量为960,一定是根据工作时间来列等量关系,本题的关键描述语是:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用20天.等量关系为:甲工厂单独加工完成这批产品天数-20=乙工厂单独加工完成这批产品的天数;
(2)设乙工厂报价为每天m元,根据乙工厂的总费用≤甲工厂的总费用,列出不等式即可求解.
解答 解:(1)设甲工厂每天加工2x件,则乙工厂每天加工3x件,由题意得:
$\frac{960}{2x}$-20=$\frac{960}{3x}$,
解得:x=8.
经检验,x=8是所列方程的根,
此时2x=16
3x=24.
答:甲工厂每天加工16台机器,乙工厂每天加工24台机器.
(2)由(1)可知加工960件产品,甲工厂要60天,乙工厂要40天.
所以甲工厂的加工总费用为60(800+50)=51000(元),
设乙工厂报价为每天m元,则乙工厂的加工总费用为40(m+50)元,
由题意得:40(m+50)≤51000,解得m≤1225.
答:乙工厂向科研所上报加工费用每天最多为1225元时,才可以满足科研所要求,有望加工这批机器.
点评 本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.注意利润率=利润成本×100%的应用.涉及到的公式:工作总量=工作效率×工作时间.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
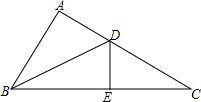 如图,△ADB≌△EDB,△BDE≌△CDE.B、E、C在一条直线上.
如图,△ADB≌△EDB,△BDE≌△CDE.B、E、C在一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
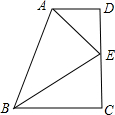 如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )
如图,在四边形ABCD中,∠C=∠D=90°,若∠DAB的平分线AE交CD于点E,连接BE,且BE恰好平分∠ABC,则下列结论中错误的是( )| A. | AE⊥BE | B. | CE=DE | C. | AD+DE=BE | D. | AB=AD+BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
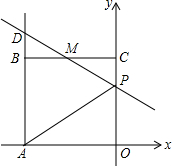 如图,已知正方形OABC的边长为4,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,n)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为4,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,n)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com