
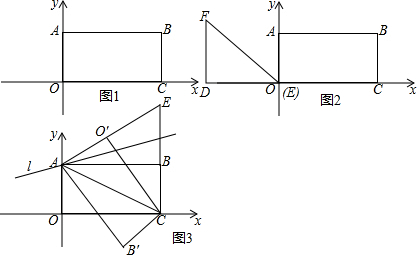
分析 (1)先画出图形,C点C恰好落在直线AB上(有C′和C″两点),在Rt△C′AO中,求出∠AC′O=30°,根据矩形的性质得出AB∥OC,求出∠C′OC+∠AC′O=180°,∠C′C″O=∠COC″,即可得出答案;
(2)分为三种情况:当0<t≤5时,②当5<t≤6时,③当6<t≤10时,画出图形,求出重叠部分面积即可;
(3)求出AE=EC,设AE=x,则EB=x-5,在Rt△EBA中,由勾股定理得出x2=102+(x-5)2,求出AE=12.5,即可求出答案;过B′作B′M⊥AP于M,过E作EN⊥AP于N,EG⊥B′M于G,得出当G和E重合时,d1+d2的值最大,求出B′E长即可.
解答 解:(1)如图1,C点C恰好落在直线AB上(有C′和C″两点),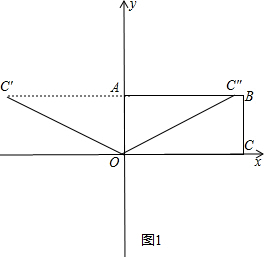
∵在Rt△C′AO中,∠C″AO=90°,OC″=OC=10,OA=5,
∴∠AC′O=30°,
∵四边形AOCB是矩形,
∴AB∥OC,
∴∠C′OC+∠AC′O=180°,∠C′C″O=∠COC″,
∴∠C′OC=150°,
∵OC′=OC″=OC=10,
∴∠AC″O=∠C′=30°,
∴∠COC″=∠AC″O=30°,
即m=150°或30°,
故答案为:150°或30°;
(2)分为三种情况:
①当0<t≤5时,如图2,设EF交OA于Q,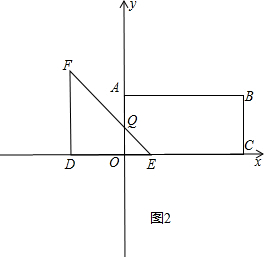
∵DF=DE,∠FDE=90°,
∴∠FED=45°,
∵四边形AOCB是矩形,
∴∠AOC=90°,
∴∠OQE=∠FEO=45°,
∴OQ=OE=t×1=t,
∴重叠部分的面积S=S△QOE=$\frac{1}{2}$t•t=$\frac{1}{2}$t2;
②当5<t≤6时,如图3,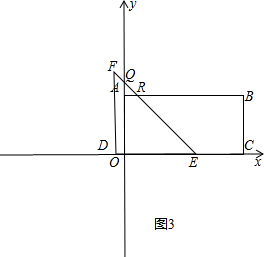
由①知:OE=OQ=t,
∵四边形AOCB是矩形,
∴AB∥OC,∠QAB=90°,
∴∠∠QRA=∠FED=45°,
∴∠AQR=∠QRA=45°,
∴AR=AQ=t-5,
∴重叠部分的面积S=S梯形AOER=$\frac{1}{2}$×(AR+OE)×OA=$\frac{1}{2}$•(t-5+t)•5,
即S=5t-12.5;
③当6<t≤10时,如图4,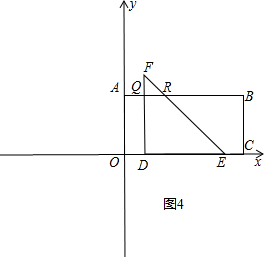
∵QF=QR=6-5=1,
∴重叠部分的面积S=$\frac{1}{2}$×(QR+DE)×DQ=$\frac{1}{2}×$(1+6)×5=17.5;
(3)如图5,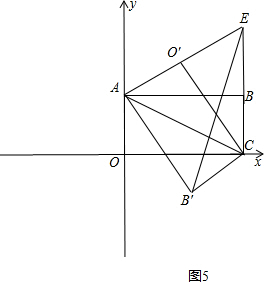
∵四边形AOCB是矩形,
∴∠OAB=90°,
∵根据折叠的性质得出AB=AB′=10,∠OAC=∠EAC,∠BAC=∠B′AC,
∴∠EAB′=∠EAC+∠B′AC=∠OAC+∠BAC=∠OAB=90°,
∵四边形AOCB是矩形,
∴OA∥BC,
∴∠ECA=∠OAC,
∵∠OAC=∠EAC,
∴∠EAC=∠ECA,
∴AE=EC,
设AE=x,则EB=x-5,
在Rt△EBA中,由勾股定理得:x2=102+(x-5)2,
解得:x=12.5,
即AE=12.5,
∴△AB′E的面积的面积是:$\frac{1}{2}$×AB′×AE=$\frac{1}{2}×$10×12.5=62.5;
如图6,过B′作B′M⊥AP于M,过E作EN⊥AP于N,EG⊥B′M于G,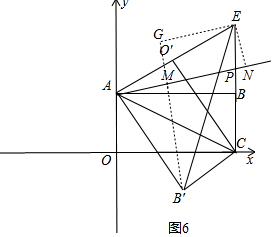
∠G=∠GMN=∠ENM=90°,
则四边形EGMN是矩形,
所以MG=EN=d1,B′M=d2,
所以d1+d2=B′G,
当G和E重合时,d1+d2的值最大,最大值是$\sqrt{1{0}^{2}+12.{5}^{2}}$=$\frac{5\sqrt{41}}{2}$.
点评 本题考查了折叠的性质,矩形的性质,等腰三角形的性质等知识点的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,难度偏大.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.
如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
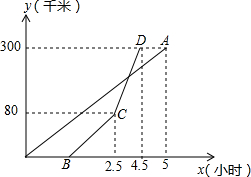 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B-C-D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下列四种说法:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B-C-D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
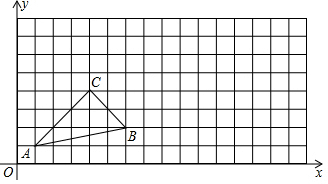 如图,△ABC中顶点A(1,1),B(6,2),C(4,4),将△ABC向右平移5个单位得到△A1B1C1,将△A1B1C1绕点B1顺时针方向旋转90°得到△A2B2C2.
如图,△ABC中顶点A(1,1),B(6,2),C(4,4),将△ABC向右平移5个单位得到△A1B1C1,将△A1B1C1绕点B1顺时针方向旋转90°得到△A2B2C2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com