
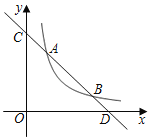
【题目】如图,已知一次函数y1=kx+b与反比例函数y2=![]() (x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求反比例函数和一次函数的解析式;
(2)求y1<y2时,自变量x的取值范围;
(3)若点P是x轴上一动点,当△ABP为直角三角形时,求点P的坐标.
【答案】(1)y2=![]() ,y1=﹣x+6;(2)0<x<2或x>4;(3)P点坐标为(﹣2,0)或(2,0).
,y1=﹣x+6;(2)0<x<2或x>4;(3)P点坐标为(﹣2,0)或(2,0).
【解析】
(1)先把A点坐标代入y2=![]() 中求出m得到反比例函数解析式为y2=
中求出m得到反比例函数解析式为y2=![]() ,再利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
,再利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
(2)在第一象限内,写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可;
(3)设P(t,0),利用两点间的距离公式得到PA2=(t﹣2)2+42,PB2=(t﹣4)2+22,AB2=(4﹣2)2+(2﹣4)2,讨论:根据勾股定理,当∠PAB=90°时,t2﹣4t+20+8=t2﹣8t+20;当∠PBA=90°时,t2﹣8t+20+8=t2﹣4t+20;当∠APB=90°时,t2﹣4t+20+t2﹣8t+20=8,然后分别解关于t的方程可得到P点坐标.
解:(1)把A(2,4)代入y2=![]() 得m=2×4=8,
得m=2×4=8,
∴反比例函数解析式为y2=![]() ,
,
把B(4,n)代入y2=![]() 得4n=8,解得n=2,则B(4,2),
得4n=8,解得n=2,则B(4,2),
把A(2,4)和B(4,2)代入y1=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数解析式为y1=﹣x+6;
(2)根据函数图象可得:当0<x<2或x>4时,y1<y2;
(3)设P(t,0),
∵A(2,4),B(4,2)
∴PA2=(t﹣2)2+42=t2﹣4t+20,PB2=(t﹣4)2+22=t2﹣8t+20,AB2=(4﹣2)2+(2﹣4)2=8,
当∠PAB=90°时,PA2+AB2=PB2,即t2﹣4t+20+8=t2﹣8t+20,解得t=﹣2,此时P点坐标为(﹣2,0),
当∠PBA=90°时,PB2+AB2=PA2,即t2﹣8t+20+8=t2﹣4t+20,解得t=2,此时P点坐标为(2,0),
当∠APB=90°时,PA2+PB2=AB2,即t2﹣4t+20+t2﹣8t+20=8,整理得t2﹣6t+16=0,方程没有实数解,
综上所述,P点坐标为(﹣2,0)或(2,0).


科目:初中数学 来源: 题型:
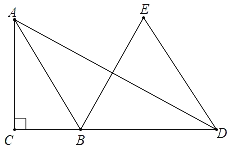
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=![]() ,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
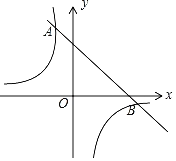
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足k1x+b>![]() 的x的取值范围.
的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,它的出现标志中国古代数学形成了完整的体系.其中有一个问题:“今有二马、一牛价过-万,如半马之价:一马、二牛价不满一万,如半牛之价.问牛、马价各几何?”其大意为:现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱:一匹马加上两头牛的价钱则不到一万,不足的部分正好是半头牛的价钱.问一头牛、一匹马各多少钱?设一匹马值![]() 钱、一头牛值
钱、一头牛值![]() 钱,则符合题意的方程组为( )
钱,则符合题意的方程组为( )
A. B.
B.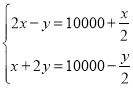
C.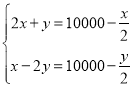 D.
D.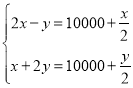
查看答案和解析>>
科目:初中数学 来源: 题型:
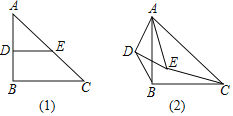
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC=4,点D、E分别是边AB、AC的中点,连接DE,将△ADE绕点A按顺时针方向旋转,记旋转角为α,BD、CE所在直线相交所成的锐角为β.
(1)问题发现当α=0°时,![]() =_____;β=_____°.
=_____;β=_____°.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 和β的大小有无变化?请仅就图2的情形给出证明.
和β的大小有无变化?请仅就图2的情形给出证明.
(3)在△ADE旋转过程中,当DE∥AC时,直接写出此时△CBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某微商销售的某商品每袋成本20元,设销售价格为x(单位:元/袋),该微商发现销售量y与销售价格x之间的关系如表:
销售价格x(元/袋) | 25 | 30 | 35 | 40 |
销售件数y | 275 | 250 | 225 | 200 |
(1)求y关于x的函数表达式;
(2)根据物价部门的规定,商品的利润率不能超过100%,该微商应该如何定价,才能使获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
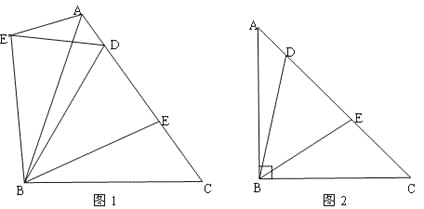
【题目】(1)如图1,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=![]() ∠ABC(0°<∠CBE<
∠ABC(0°<∠CBE<![]() ∠ABC).以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE′A(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
∠ABC).以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE′A(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
(2)如图2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,
且满足∠DBE=![]() ∠ABC(0°<∠CBE<45°) .求证:DE2=AD2+EC2.
∠ABC(0°<∠CBE<45°) .求证:DE2=AD2+EC2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,直线
,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 交于点
交于点![]() .
.
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若![]() 的面积为6,求直线CD的表达式.
的面积为6,求直线CD的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com