
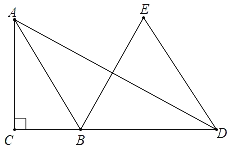
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=![]() ,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
【答案】![]() .
.
【解析】
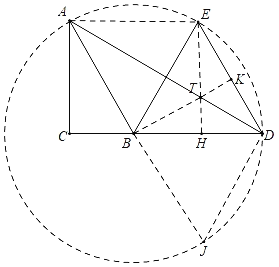
如图,在线段DA上取一点T,使得DT=TE,连接ET,BT,AE,延长BT交DE于K,作TH⊥BD于H.想办法证明∠EAB=![]() ∠EBD,推出点A在B为圆心,BE为半径的⊙B上,延长AB交⊙B于J,连接DJ.解直角三角形求出TK,DK即可解决问题.
∠EBD,推出点A在B为圆心,BE为半径的⊙B上,延长AB交⊙B于J,连接DJ.解直角三角形求出TK,DK即可解决问题.
解:如图,在线段DA上取一点T,使得DT=TE,连接ET,BT,AE,延长BT交DE于K,作TH⊥BD于H.
∵△BDE是等边三角形,
∴BE=BD,∠EBD=60°,
∵TE=TD,BT=BT,
∴△BTE≌△BTD(SSS),
∴∠EBT=∠DBT=30°,
∵BE=BD,
∴BK⊥DE,EK=DK,
∵TE=TD,
∴∠TED=∠TDE,
∴∠ATE=∠TED+∠TDE=2∠TDE,
∵∠ABE=2∠ADE,
∴∠ABE=∠ATE,
∴A,B,T,E四点共圆,
∴∠EAT=∠EBT=30°,
∴∠EAB=![]() ∠EBD,
∠EBD,
∴点A在B为圆心,BE为半径的⊙B上,延长AB交⊙B于J,连接DJ.
∵AJ是直径,
∴∠ADJ=90°,
∴DJ=![]()
∴tan∠DAJ=![]() ,
,
∵BA=BD,
∴∠BDA=∠BAD,
∴tan∠BDA=![]() ,
,
∵TH⊥DH,
∴![]() =
=![]() ,设TH=
,设TH=![]() k,则DH=11k,
k,则DH=11k,
在Rt△BHT中,BH=![]() =9k,
=9k,
∴BD=BH+DH=20k=![]() ,
,
∴k=![]() ,
,
∴BT=2TH=![]() ,
,
∵BK=BDcos30°=![]() ,
,
∴TK=BK﹣BT=![]() ,
,
∵DK=![]() ,
,
∴tan∠ADE=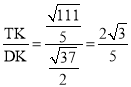 .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() :
:![]() (
(![]() ,
,![]() 是常数)经过
是常数)经过![]() 、
、![]() 两点.
两点.
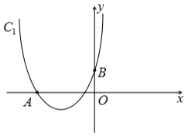
(1)求![]() ,
,![]() 的值;
的值;
(2)向右平移抛物线![]() ,使它经过点
,使它经过点![]() ,得抛物线
,得抛物线![]() ,
,![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,且在另一个交点的左侧.
,且在另一个交点的左侧.
①求抛物线![]() 的表达式;
的表达式;
②![]() 是点
是点![]() 关于抛物线
关于抛物线![]() 对称轴的对称点,
对称轴的对称点,![]() 是线段
是线段![]() 上一点,
上一点,![]() 轴,交抛物线
轴,交抛物线![]() 于点
于点![]() ,
,![]() 为垂足,设
为垂足,设![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 的值,使
的值,使![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() (x>0) 的图像经过矩形ABCD的顶点A、C,AC的垂直平分线分别交AB、CD于点P、Q;己知点B坐标为(1,2),矩形ABCD的面积为8.
(x>0) 的图像经过矩形ABCD的顶点A、C,AC的垂直平分线分别交AB、CD于点P、Q;己知点B坐标为(1,2),矩形ABCD的面积为8.
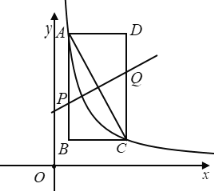
(1)求k的值;
(2)求直线PQ的解析式;
(3)连接PC、AQ,判断四边形APC Q的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级男生“跳绳”成绩的情况,随机选取该年级部分男生进行测试.以下是根据测试成绩绘制的统计图表的一部分.
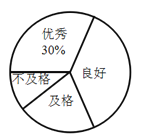
成绩等级 | 频数(人) | 频率 |
优秀 | ||
良好 | ||
及格 | 10 | 0.2 |
不及格 | 0.1 |
根据以上信息,解答下列问题:
(1)被测试男生中,成绩等级为“优秀”的男生人数占被测试男生总人数的百分比为________%,成绩等级为“及格”的男生人数为________人;
(2)被测试男生的总人数为________人,成绩等级为“不及格”的男生人数________人;
(3)若该校七年级共有570名男生,根据调查结果,估计该校七年级男生成绩等级为“良好”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“只要人人都献出一点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂捐款”活动倡议,有2500名居民踊跃参与献爱心.社区管理员随机抽查了部分居民捐款情况,统计图如图:

(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人?
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形![]() 折叠,使顶点
折叠,使顶点![]() 与
与![]() 边上的一点
边上的一点![]() 重合(
重合(![]() 不与端点
不与端点![]() ,
,![]() 重合),折痕交
重合),折痕交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,边
,边![]() 折叠后与边
折叠后与边![]() 交于点
交于点![]() ,设正方形
,设正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,则
,则![]() 的值为( )
的值为( )
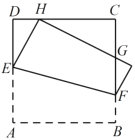
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=3;
③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;
④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6![]() .
.
其中真命题的序号是____________.
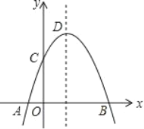
查看答案和解析>>
科目:初中数学 来源: 题型:
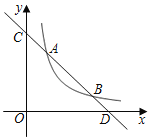
【题目】如图,已知一次函数y1=kx+b与反比例函数y2=![]() (x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求反比例函数和一次函数的解析式;
(2)求y1<y2时,自变量x的取值范围;
(3)若点P是x轴上一动点,当△ABP为直角三角形时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com